
【题目】已知,数轴上点![]() 、
、![]() 对应的数分别为
对应的数分别为![]() 、
、![]() ,且满足
,且满足![]() ,点
,点![]() 对应点的数为-3.
对应点的数为-3.
(1)![]() ______,
______,![]() ______;
______;
(2)若动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发向右运动,点
同时出发向右运动,点![]() 的速度为3个单位长度/秒;点
的速度为3个单位长度/秒;点![]() 的速度为1个单位长度/秒,求经过多长时间
的速度为1个单位长度/秒,求经过多长时间![]() 、
、![]() 两点的距离为
两点的距离为![]() ;
;
(3)在(2)的条件下,若点![]() 运动到点
运动到点![]() 立刻原速返回,到达点
立刻原速返回,到达点![]() 后停止运动,点
后停止运动,点![]() 运动至点
运动至点![]() 处又以原速返回,到达点
处又以原速返回,到达点![]() 后又折返向
后又折返向![]() 运动,当点
运动,当点![]() 停止运动点
停止运动点![]() 随之停止运动.求在整个运动过程中,两点
随之停止运动.求在整个运动过程中,两点![]() ,
,![]() 同时到达的点在数轴上表示的数.
同时到达的点在数轴上表示的数.

【答案】(1)-7,1.(2)经过![]() 秒或
秒或![]() 秒
秒![]() ,
,![]() 两点的距离为
两点的距离为![]() .(3)在整个运动过程中,两点
.(3)在整个运动过程中,两点![]() ,
,![]() 同时到达的点在数轴上表示的数分别是-1,0,-2.
同时到达的点在数轴上表示的数分别是-1,0,-2.
【解析】
(1)由绝对值和偶次方的非负性列方程组可解;
(2)设经过t秒两点的距离为![]() ,根据题意列绝对值方程求解即可;
,根据题意列绝对值方程求解即可;
(3)分类讨论:点P未运动到点C时;点P运动到点C返回时;当点P返回到点A时.分别求出不同阶段的运动时间,进而求出相关点所表示的数即可.
(1)由非负数的性质可得:![]() ,
,
∴![]() ,
,![]() ,
,
故答案为:-7,1;
(2)设经过![]() 秒两点的距离为
秒两点的距离为![]() ,
,
由题意得:![]() ,
,
解得![]() 或
或![]() ,
,
答:经过![]() 秒或
秒或![]() 秒
秒![]() ,
,![]() 两点的距离为
两点的距离为![]() ;
;
(3)点![]() 未运动到点
未运动到点![]() 时,设经过
时,设经过![]() 秒
秒![]() ,
,![]() 相遇,
相遇,
由题意得:![]() ,
,
∴![]() ,
,
表示的数为:![]() ,
,
点![]() 运动到点
运动到点![]() 返回时,设经过
返回时,设经过![]() 秒
秒![]() ,
,![]() 相過,
相過,
由题意得:![]() ,
,
∴![]() ,
,
表示的数是:![]() ,
,
当点![]() 返回到点
返回到点![]() 时,用时
时,用时![]() 秒,此时点
秒,此时点![]() 所在位置表示的数是
所在位置表示的数是![]() ,
,
设再经过![]() 秒相遇,
秒相遇,
由题意得:![]() ,
,
∴![]() ,
,
表示的数是:![]() ,
,
答:在整个运动过程中,两点![]() ,
,![]() 同时到达的点在数轴上表示的数分别是-1,0,-2.
同时到达的点在数轴上表示的数分别是-1,0,-2.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G.使得∠EGB=∠EAB,连接AG.
求证:EG=AG+BG.
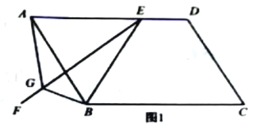
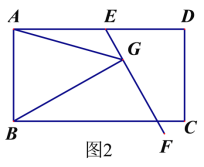
小明同学的思路是:作∠CAM=∠EAB交CE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EC、AG、BG之间的数量关系,并证明你的结论.
解:线段EG、AG、BG之间的数量关系为___________________________________________________.证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人在一次射击比赛中击中靶的情况(击中靶中心“×”所在的圆面为10环,靶中各数字表示该数所在圆环被击中所得的环数),每人射击了6次.
(1)请用列表法将他俩的射击成绩统计出来;
(2)请你运用所学的统计知识做出分析,从两个不同角度评价甲、乙两人的打靶成绩.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C![]() 90°,AC
90°,AC![]() BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
BC,AD是△ABC的角平分线,以D为圆心,DC为半径作⊙D,交AD于点E.
(1)判断直线AB与⊙D的位置关系并证明.
(2)若AC![]() 1,求
1,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P在函数![]() 的图象上,过P作直线
的图象上,过P作直线![]() 轴于点A,交直线
轴于点A,交直线![]() 于点M,过M作直线
于点M,过M作直线![]() 轴于点B.交函数
轴于点B.交函数![]() 的图象于点Q。
的图象于点Q。
(1)若点P的横坐标为1,写出点P的纵坐标,以及点M的坐标;
(2)若点P的横坐标为t,
①求点Q的坐标(用含t的式子表示)
②直接写出线段PQ的长(用含t的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案
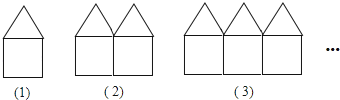
(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE= ;
(2)如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com