
分析 (1)利用单项式乘以单项式及单项式除以单项式法则计算,即可得到结果;
(2)根据二次根式的加减运算法则进行解答即可.
解答 解:(1)原式=5×(-$\frac{1}{10}$)x2+1y2+3-$\frac{1}{2}$×(-$\frac{1}{2}$)x2+1y1+4
=-$\frac{1}{2}$x3y5+$\frac{1}{4}$x3y5
=$-\frac{1}{4}{x^3}{y^5}$;
(2)原式=$\frac{2}{3}$×3$\sqrt{x}$-$\frac{6}{2}$$\sqrt{x}$+2$\sqrt{x}$=(2-3+2)$\sqrt{x}$=$\sqrt{x}$.
点评 此题考查了二次根式的加减法,单项式乘单项式.熟记计算法则即可解题,属于基础题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小亮在操场上玩,一段时间内沿M→A→B→M的路径匀速散步,能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是( )
如图,小亮在操场上玩,一段时间内沿M→A→B→M的路径匀速散步,能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
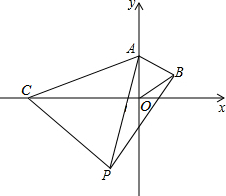 如图,在直角坐标系中,点A的坐标是(0,2),点C是x轴上的一个动点,点C在x轴上移动时,始终保持△ACP是等边三角形,当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
如图,在直角坐标系中,点A的坐标是(0,2),点C是x轴上的一个动点,点C在x轴上移动时,始终保持△ACP是等边三角形,当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
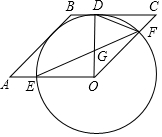 已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.
已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-8)与+(+8) | B. | -(+8)与-|-8| | C. | -|-8|与+(-8) | D. | -22与(-2)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com