
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 于点
于点![]() ,连
,连![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ..其中正确结论的个数为( )
..其中正确结论的个数为( )

A. 5 B. 4 C. 3 D. 2
【答案】B
【解析】①由等边三角形与等腰直角三角形知△CAD是等腰三角形且顶角∠CAD=150°,据此可判断;②求出∠AFP和∠FAG度数,从而得出∠AGF度数,据此可判断;③证△ADF≌△BAH即可判断;④由∠AFG=∠CBG=60°、∠AGF=∠CGB即可得证;⑤设PF=x,则AF=2x、AP=![]() x,设EF=a,由△ADF≌△BAH知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得
x,设EF=a,由△ADF≌△BAH知BH=AF=2x,根据△ABE是等腰直角三角形之BE=AE=a+2x,据此得出EH=a,证△PAF∽△EAH得![]() ,从而得出a与x的关系即可判断.
,从而得出a与x的关系即可判断.
∵△ABC为等边三角形,△ABD为等腰直角三角形,
∴∠BAC=60°、∠BAD=90°、AC=AB=AD,∠ADB=∠ABD=45°,
∴△CAD是等腰三角形,且顶角∠CAD=150°,
∴∠ADC=15°,故①正确;
∵AE⊥BD,即∠AED=90°,
∴∠DAE=45°,
∴∠AFG=∠ADC+∠DAE=60°,∠FAG=45°,
∴∠AGF=75°,
由∠AFG≠∠AGF知AF≠AG,故②错误;
记AH与CD的交点为P,

由AH⊥CD且∠AFG=60°知∠FAP=30°,
则∠BAH=∠ADC=15°,
在△ADF和△BAH中,
∵ ,
,
∴△ADF≌△BAH(ASA),
∴DF=AH,故③正确;
∵∠AFG=∠CBG=60°,∠AGF=∠CGB,
∴△AFG∽△CBG,故④正确;
在Rt△APF中,设PF=x,则AF=2x、AP=![]() x,
x,
设EF=a,
∵△ADF≌△BAH,
∴BH=AF=2x,
△ABE中,∵∠AEB=90°、∠ABE=45°,
∴BE=AE=AF+EF=a+2x,
∴EH=BE-BH=a+2x-2x=a,
∵∠APF=∠AEH=90°,∠FAP=∠HAE,
∴△PAF∽△EAH,
∴![]() ,即
,即![]() ,
,
整理,得:2x2=(![]() -1)ax,
-1)ax,
由x≠0得2x=(![]() -1)a,即AF=(
-1)a,即AF=(![]() -1)EF,故⑤正确;
-1)EF,故⑤正确;
故选:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
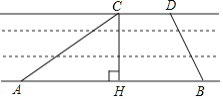
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含有 30°角的直角三角板 OAB 如图放置在平面直角坐标系中,OB 在 x轴上,若 OA=2,将三角板绕原点 O 顺时针旋转 75°,则点 A 的对应点 A′ 的坐标为___________.
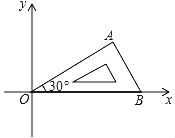
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,点E在弦AB所对的优弧上,且![]() 为半圆,C是
为半圆,C是![]() 上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
上的动点,连接CA、CB,已知AB=4cm,设B、C间的距离为xcm,点C到弦AB所在直线的距离为y1cm,A、C两点间的距离为y2cm.
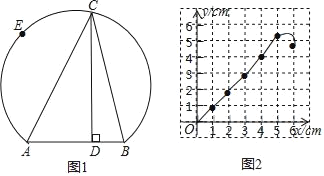
小明根据学习函数的经验,分别对函数y1、y2岁自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整.
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1、y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 0.78 | 1.76 | 2.85 | 3.98 | 4.95 | 4.47 |
y2/cm | 4 | 4.69 | 5.26 | 5.96 | 5.94 | 4.47 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1、y2的图象;
(3)结合函数图象,解决问题:
①连接BE,则BE的长约为 cm.
②当以A、B、C为顶点组成的三角形是直角三角形时,BCspan>的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】袋中装有除数字不同其它都相同的六个小球,球上分别标有数字1,2,3,4,5,6.
(1)从袋中摸出一个小球,求小球上数字小于3的概率;
(2)将标有1,2,3数字的小球取出放入另外一个袋中,分别从两袋中各摸出一个小球,
求数字之和为偶数的概率.(要求用列表法或画树状图求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等的凸四边形叫做“准菱形”.利用该定义完成以下各题:
(1) 理解
填空:如图1,在四边形ABCD中,若 (填一种情况),则四边形ABCD是“准菱形”;
(2)应用
证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,求证并证明)
(3) 拓展
如图2,在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF,连接AD,BF,若平移后的四边形ABFD是“准菱形”,求线段BE的长.
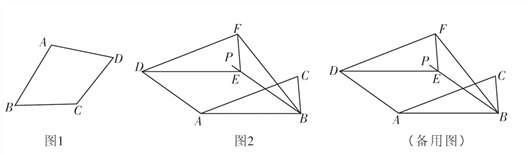
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,无人机航拍测量的应用越来越广泛.如图,无人机从A处观测得某建筑物顶点O时俯角为30°,继续水平前行10米到达B处,测得俯角为45°,已知无人机的水平飞行高度为45米,则这栋楼的高度是多少米?(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com