
| 5 |
| 4 |
| 3 |
| 5 |
8
| ||
| 3 |
| 5 |
2
| ||
| 2 |
| 5 |
| QM |
| PM |
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
| 9 |
| 2 |
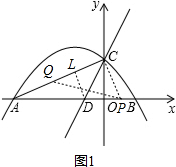 解:(1)依题意可得
解:(1)依题意可得
|
|
| 1 |
| 8 |
| 1 |
| 2 |
| 4 |
| 3 |
| DL |
| 4 |
| AL |
| 8 |
| ||
4
|
| 4 |
| 3 |
| 5 |
| 8 |
| 3 |
| 5 |
| 5 |
| 4 |
| 3 |
| 5 |
8
| ||
| 3 |
| 5 |
| 5 |
2
| ||
| 2 |
| 5 |
| PN |
| NQ |
| NA |
| PN |
| 1 |
| 2 |
| QM |
| PM |
| 1 |
| 2 |
| QH |
| MG |
| HM |
| PG |
| QM |
| PM |
| 1 |
| 2 |
|
|
| 1 |
| 8 |
| 1 |
| 2 |
| 9 |
| 2 |


科目:初中数学 来源: 题型:
 如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
如图是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )| A、a2+b2 |
| B、4ab |
| C、(b+a)2-4ab |
| D、b2-a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| x+1 |
| 4 |
| x-3 |
|
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
查看答案和解析>>
科目:初中数学 来源: 题型:
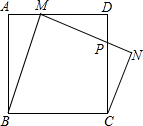 如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=
如图,正方形ABCD中,M为边AD的一动点(不与点A、D重合),作等腰梯形BMNC,其中BM∥CN,BC=MN,MN与CD交于点P,若AB=1,AM=x,CP=y,则y关于x的函数关系式为y=查看答案和解析>>
科目:初中数学 来源: 题型:
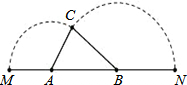 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,若△ABC为直角三角形,则x=
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC.设AB=x,若△ABC为直角三角形,则x=查看答案和解析>>
科目:初中数学 来源: 题型:
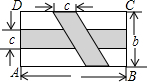 如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是
如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com