
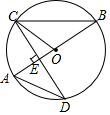
 如图,AB是圆O的直径.CD是圆O的一条弦.且CD⊥AB于点E.
如图,AB是圆O的直径.CD是圆O的一条弦.且CD⊥AB于点E.分析 (1)首先求出∠ADE的度数,再根据圆周角定理求出∠AOC的度数,最后求出∠OCE的度数;
(2)由弦CD与直径AB垂直,利用垂径定理得到E为CD的中点,求出CE的长,在直角三角形OCE中,设圆的半径OC=r,OE=OA-AE,表示出OE,利用勾股定理列出关于r的方程,求出方程的解即可得到圆的半径r的值,根据弧长的公式即可得到结论.
解答 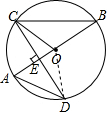 解:(1)∵CD⊥AB,∠A=48°,
解:(1)∵CD⊥AB,∠A=48°,
∴∠ADE=42°.
∴∠AOC=2∠ADE=84°,
∴∠OCE=90°-84°=6°;
(2)解:因为AB是圆O的直径,且CD⊥AB于点E,所以CE=$\frac{1}{2}$CE=$\frac{1}{2}$×4$\sqrt{2}$=2$\sqrt{2}$,
在Rt△OCE中,OC2=CE2+OE2,
设圆O的半径为r,则OC=r,OE=OA-AE=r-2,所以r2=(2$\sqrt{2}$)2+(r-2)2,
解得:r=3.
∴圆O的半径为3,
连接OD,
∴∠BOD=2∠A=96°,
∴$\widehat{BD}$的长=$\frac{96•π×{3}^{2}}{360}$=$\frac{12}{5}$π.
点评 本题考查了弧长的计算,圆周角定理,垂径定理,正确的作出辅助线是解题的关键.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
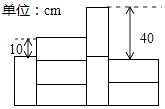 如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是525cm2.
如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10cm,两块横放的墙砖比两块竖放的墙砖低40cm,则每块墙砖的截面面积是525cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
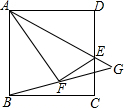 如图,正方形ABCD中,E是CD的中点,连接AE,沿AE折叠,使得点D落在正方形内的点F处,连接BF并延长,交AE的延长线于点G.
如图,正方形ABCD中,E是CD的中点,连接AE,沿AE折叠,使得点D落在正方形内的点F处,连接BF并延长,交AE的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
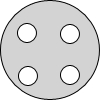 如图,在半径为R的圆形钢板上冲去半径r的四个小圆孔,若R=8.6cm,r=0.7cm,请你利用因式分解的方法计算出剩余钢板的面积.(π取3.14)
如图,在半径为R的圆形钢板上冲去半径r的四个小圆孔,若R=8.6cm,r=0.7cm,请你利用因式分解的方法计算出剩余钢板的面积.(π取3.14)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
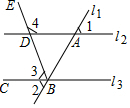 如图所示,直线l1与l2,l3相交于A,B两点,∠ABC的平分线交l2于点D,已知∠1=∠2=62°.
如图所示,直线l1与l2,l3相交于A,B两点,∠ABC的平分线交l2于点D,已知∠1=∠2=62°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间(分钟) | 里程数(千米) | 车费(元) | |
| 小明 | 7 | 5 | 12.1 |
| 小亮 | 6 | 4.5 | 10.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com