
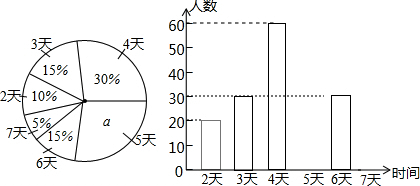
分析 (1)用1减去已知的各个百分比,求得a的值,再用人数除以相应的百分比,求得该校七年级学生总人数;
(2)先根据百分比乘上总人数,求得“活动时间为5天”和“活动时间为7天”的人数,再进行画图;
(3)根据统计图,用“活动时间为4天”的百分比乘上360°,求得扇形的圆心角的度数;
(4)根据“活动时间不少于4天”的百分比之和,乘上该市七年级学生总数,求得该市“活动时间不少于4天”的七年级学生数.
解答 解:(1)a=1-10%-15%-30%-15%-5%=25%,该校七年级学生总人数=20÷10%=200(人),
故答案为:25%,200;
(2)“活动时间为5天”的人数为:25%×200=50(人),
“活动时间为7天”的人数为:5%×200=10(人),
条形统计图如下: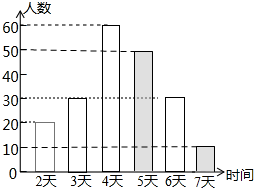
(3)“活动时间为4天”的扇形的圆心角的度数=30%×360°=108°,
故答案为:108°;
(4)(30%+25%+15%+5%)×6000=4500,
故“活动时间不少于4天”的大约有4500人.
点评 本题主要考查了扇形统计图与条形统计图,计算时注意,各部分扇形圆心角的度数=部分占总体的百分比×360°.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.


科目:初中数学 来源: 题型:选择题
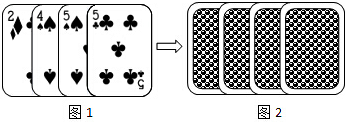
 某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )
某小组在“用频率估计概率”的试验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的试验最有可能的是( )| A. | 在装有1个红球和2个白球(除颜色外完全相同)的不透明袋子里随机摸出一个球是“白球” | |
| B. | 从一副扑克牌中任意抽取一张,这张牌是“红色的” | |
| C. | 掷一枚质地均匀的硬币,落地时结果是“正面朝上” | |
| D. | 只一个质地均匀的正六面体骰子,落地时面朝上的点数是6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k | B. | $\frac{1}{2}$k | C. | k2 | D. | $\frac{1}{2}$k2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com