
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE等于多少时时,四边形BFCE是菱形.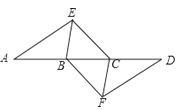
【答案】证明:(1)∵AB=DC,
∴AC=DB,
在△AEC和△DFB中 ,
,
∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF
∴EC∥BF,
∴四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,
∵AD=10,DC=3,AB=CD=3,
∴BC=10﹣3﹣3=4,
∵∠EBD=60°,
∴BE=BC=4,
∴当BE=4 时,四边形BFCE是菱形,
故答案为:4.
【解析】(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.


科目:初中数学 来源: 题型:
【题目】如图,要得到AB∥CD,只需要添加一个条件,这个条件不可以是( )
A.∠1=∠3
B.∠B+∠BCD=180°
C.∠2=∠4
D.∠D+∠BAD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外兴趣小组为了了解所在学校的学生对体育运动的爱好情况,设计了四种不同的抽样调查方案,你认为比较合理的是( )
A. 在校园内随机选择50名学生
B. 从运动场随机选择50名男生
C. 从图书馆随机选择50名女生
D. 从七年级学生中随机选择50名学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下叙述正确的有( )
①在同一平面内,不相交的两条直线互相平行;②有公共顶点且有一条公共边的两个角互为邻补角;③如果两条直线被第三条直线所截,那么同位角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com