

分析 (1)∠D=∠BCD=90°,求出∠DAF=∠DCE=55°,即可得出结果;
(2)作BM⊥AF于M,BN⊥EF于N,由三角函数得出MF=BN=BC•sin35°≈4.59(cm),AM=AB•cos35°≈8.20,(cm),即可得出结果.
解答 解:(1)∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,
∴∠DAF=∠DCE=90°-35°=55°
∴∠BAF=90°-55°=35°;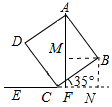 (2)作BM⊥AF于M,BN⊥EF于N,如图所示:
(2)作BM⊥AF于M,BN⊥EF于N,如图所示:
则MF=BN=BC•sin35°=0.5736×8≈4.59(cm),
AM=AB•cos35°=10×0.8192≈8.20,(cm),
∴AF=AM+MF=8.20+4.59≈12.8(cm);
即A到水平直线CE的距离AF的长为12.8cm.
点评 本题考查了解直角三角形的应用;通过作辅助线运用三角函数求出AM和BN是解决问题的关键.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
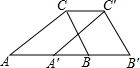 如图,在△ABC中,AB=4,将△ABC沿射线AB方向平移得到△A′B′C′,连接CC′,若A′C′恰好经过BC边的中点D,则AB′的长度为6.
如图,在△ABC中,AB=4,将△ABC沿射线AB方向平移得到△A′B′C′,连接CC′,若A′C′恰好经过BC边的中点D,则AB′的长度为6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
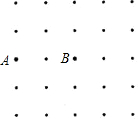 如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.
如图,由25个点构成的5×5的正方形点阵中,横纵方向相邻的两点之间的距离都是1个单位.定义:由点阵中四个点为顶点的平行四边形叫阵点平行四边形.图中以A,B为顶点,面积为2的阵点平行四边形的个数为9个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,∠AOD=90°.
如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,∠AOD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,三角形ABC在平面直角坐标系中,
如图,三角形ABC在平面直角坐标系中,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com