
 如图,已知点P(m,5)在直线y=kx(k>0)上,线段OP的垂直平分线交y轴于点A,交x轴于点B,连接AP,BP,得“筝形”四边形PAOB.
如图,已知点P(m,5)在直线y=kx(k>0)上,线段OP的垂直平分线交y轴于点A,交x轴于点B,连接AP,BP,得“筝形”四边形PAOB.分析 (1)过点P作PE⊥OA,求出点P坐标,从而得到PE=2,OE=5即可;
(2)先确定出直线OP解析式,从而求出直线AB解析式,即求出四边形PAOB的面积,令x=5,求出三角形BCD的面积,再用作差法求出函数关系式,即可.
解答 解:(1)如图,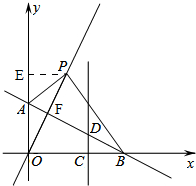
∵PE⊥OA,
∵m=2,
∴P(2,5),
∴PE=2,OE=5,
在Rt△OPE中,tan∠POA=$\frac{PE}{OE}$=$\frac{2}{5}$.
(2)S>2t+$\frac{75}{4}$
理由:∵P(m,5)在直线y=kx上,
∴5=mk,F($\frac{m}{2}$,$\frac{5}{2}$)
∴k=$\frac{5}{m}$,
∵线段OP的垂直平分线交y轴于点A,交x轴于点B,
∴直线AB解析式为y=-$\frac{m}{5}$x+$\frac{5}{2}+\frac{{m}^{2}}{10}$,
∴A(0,$\frac{5}{2}+\frac{{m}^{2}}{10}$),B($\frac{25}{2m}+\frac{m}{2}$,0),
∴OA=$\frac{5}{2}+\frac{{m}^{2}}{10}$,OB=$\frac{25}{2m}+\frac{m}{2}$,
∴S=2×$\frac{1}{2}$×($\frac{5}{2}+\frac{{m}^{2}}{10}$)($\frac{25}{2m}+\frac{m}{2}$)=($\frac{5}{2}+\frac{{m}^{2}}{10}$)($\frac{25}{2m}+\frac{m}{2}$)
∵直线x=5交x轴于点C,
∴令x=5,则有y=-$\frac{m}{5}$×5+$\frac{5}{2}+\frac{{m}^{2}}{10}$=-m+$\frac{5}{2}+\frac{{m}^{2}}{10}$,
∴CD=-m+$\frac{5}{2}+\frac{{m}^{2}}{10}$,BC=$\frac{25}{2m}+\frac{m}{2}$-5,
∴2t+$\frac{75}{4}$=2×$\frac{1}{2}$($\frac{25}{2m}+\frac{m}{2}$-5)(-m+$\frac{5}{2}+\frac{{m}^{2}}{10}$)+$\frac{75}{4}$=($\frac{25}{2m}+\frac{m}{2}$-5)(-m+$\frac{5}{2}+\frac{{m}^{2}}{10}$)+$\frac{75}{4}$=($\frac{5}{2}+\frac{{m}^{2}}{10}$)($\frac{25}{2m}+\frac{m}{2}$)-[(m-$\frac{5}{2}$)2+$\frac{75}{4}$],
∴S-(2t+$\frac{75}{4}$)=($\frac{5}{2}+\frac{{m}^{2}}{10}$)($\frac{25}{2m}+\frac{m}{2}$)-{($\frac{5}{2}+\frac{{m}^{2}}{10}$)($\frac{25}{2m}+\frac{m}{2}$)-[(m-$\frac{5}{2}$)2+$\frac{75}{4}$]}=(m-$\frac{5}{2}$)2+$\frac{75}{4}$>0,
∴S>2t+$\frac{75}{4}$.
点评 此题是一次函数综合题,主要考查了坐标的特点,线段的长,用m表示出筝形的面积,和三角形的面积,解本题的关键是用m表示出OA,OB,CD,BC.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | C. | 2÷$\sqrt{2}$=$\sqrt{2}$ | D. | 2$\sqrt{2}$-$\sqrt{2}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,这样可以用来说明我们学习过的定理或者公式是( )
如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′.设AB=a,BC=b,AC=c,这样可以用来说明我们学习过的定理或者公式是( )| A. | 勾股定理 | B. | 平方差公式 | ||
| C. | 完全平方公式 | D. | 以上3个答案都可以 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向东走了30米 | B. | 向西走了30米 | C. | 向东走了110米 | D. | 向西走了-30米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com