
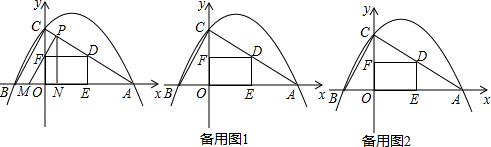
���� ��1�����ô���ϵ�������ɽ�����⣮
��2������P���D�غ�ʱ����ͼ1�У�����N���E�غϣ���ʱPN=$\sqrt{3}$������PM=$\frac{1}{2}$AM=4-t�г����̼��ɽ����
��3��������������ͼ1�У���0��t$��\frac{1}{2}$ʱ����PN��DF�ڵ�H���ص�����SΪ����FONH�����������ͼ2�У���$\frac{1}{2}$��t��1ʱ����PM��DF�ڵ�G����FO�ڵ�K��PN��DF�ڵ�H�����ص�����SΪ�����ONHGK�����������ͼ3�У���1��1��2ʱ����PM��DF�ڵ�G��PN��DF�ڵ�H�����ص�����SΪ�ı���MNHG�������
�ֱ���⼴�ɣ��ٸ��ݺ�������������ֵ��
��� �⣺��1����������y=a��x-2��2+h��A��6��0����C��0��2$\sqrt{3}$������$\left\{\begin{array}{l}{4a+h=2\sqrt{3}}\\{16a+h=0}\end{array}\right.$���$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{6}}\\{h=\frac{8\sqrt{3}}{3}}\end{array}\right.$��
�������߽���ʽΪy=-$\frac{\sqrt{3}}{6}$��x-2��2+$\frac{8\sqrt{3}}{3}$��
��2����$OB=2��OC=2\sqrt{3}$��OA=6��
���CBA=60�㣬��BAC=30�㣬
��BC��PM��
���APM=��ACB=90�㣬��PMA=60�㣬
��BM=2t��
��AM=8-2t��PM=$\frac{1}{2}$AM=4-t��
��D��AC�е㣬
��DE=$\sqrt{3}$��
����P���D�غ�ʱ����ͼ1�У�����N���E�غϣ���ʱPN=$\sqrt{3}$��
��PM=2����4-t=2��
��t=2��
��3�����ı���DEOF�Ǿ��Σ�
��DE=OF=$\sqrt{3}$��
�ɣ�2����֪BM=2t��PM=4-t��
��MN=$\frac{1}{2}$PM=2-$\frac{1}{2}$t��
BN=2t+2-$\frac{1}{2}$t=2+$\frac{3}{2}$t��ON=BN-BO=$\frac{3}{2}$t��
����ͼ1�У���0��t$��\frac{1}{2}$ʱ����PN��DF�ڵ�H���ص�����SΪ����FONH�������
��S=ON•OF=$\sqrt{3}$��$\frac{3}{2}$t=$\frac{3\sqrt{3}}{2}$t��
��S��t�����������
�൱t=$\frac{1}{2}$ʱ��S���=$\frac{3\sqrt{3}}{4}$��
����ͼ2�У���$\frac{1}{2}$��t��1ʱ����PM��DF�ڵ�G����FO�ڵ�K��PN��DF�ڵ�H�� ���ص�����SΪ�����ONHGK�������
���ص�����SΪ�����ONHGK�������
��MO=2-2t��
��KO=��2-2t��tan60��=2$\sqrt{3}$-2$\sqrt{3}$t��
��FK=$\sqrt{3}$-��2$\sqrt{3}$-2$\sqrt{3}$t��=$\sqrt{3}$��2t-1����
S=S����ONHF-S��FGK=$\sqrt{3}$��$\frac{3}{2}$t-$\frac{\sqrt{3}}{2}$��2t-1����2t-1��=-2$\sqrt{3}$t2+$\frac{7\sqrt{3}}{2}$t-$\frac{\sqrt{3}}{2}$=-2$\sqrt{3}$��t-$\frac{7}{8}$��2+$\frac{33\sqrt{3}}{32}$��
�൱t=$\frac{7}{8}$ʱ��S���=$\frac{33\sqrt{3}}{32}$��
����ͼ3�У���1��1��2ʱ����PM��DF�ڵ�G��PN��DF�ڵ�H�����ص�����SΪ�ı���MNHG�������
��PN=PMcos60��=$\frac{\sqrt{3}}{2}$��4-t������PH=$\frac{\sqrt{3}}{2}$��4-t��-$\sqrt{3}$=$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t��
��GH=$\frac{\sqrt{3}}{3}$��$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t��=1-$\frac{1}{2}$t��
��S=$\frac{1}{2}$[��1-$\frac{1}{2}$t��+��2-$\frac{1}{2}$t��]��$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$t��
��-$\frac{\sqrt{3}}{2}$��0��
��S��t���������
��t=1ʱ��S���=$\sqrt{3}$��
��������S=$\left\{\begin{array}{l}{\frac{3\sqrt{3}}{2}t}&{��0��t��\frac{1}{2}��}\\{-2\sqrt{3}{t}^{2}+\frac{7\sqrt{3}}{2}t-\frac{\sqrt{3}}{2}}&{��\frac{1}{2}��t��1��}\\{-\frac{\sqrt{3}}{2}t+\frac{3\sqrt{3}}{2}}&{��1��t��2��}\end{array}\right.$����t=$\frac{7}{8}$ʱ��S���=$\frac{33\sqrt{3}}{32}$��
���� ���⿼����κ����ۺ��⡢���ε����ʡ������Ρ�����ε���������֪ʶ������Ĺؼ���������մ���ϵ����ȷ����������ʽ��ѧ����ȷ����ͼ�Σ�����ֶκ����Ľ���ʽ�������п�ѹ���⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ������������й����������������е��г�һ��ƽ�棬�γ���ͼ��ʾ�ļ����壬����ȷ��չ��ͼΪ��������
������������й����������������е��г�һ��ƽ�棬�γ���ͼ��ʾ�ļ����壬����ȷ��չ��ͼΪ��������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�O�У�ABΪֱ����D��EΪԲ�����㣬CΪԲ��һ�㣬�ҡ�E+��C=90�㣮
��ͼ���ڡ�O�У�ABΪֱ����D��EΪԲ�����㣬CΪԲ��һ�㣬�ҡ�E+��C=90�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
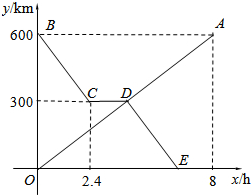 �����ͽγ��ֱ�Ӽס�������ͬʱ��������ͬһ��·������У��γ�����2.4h����Ϣ��ֱ���������������ԭ�ٶȼ�����ʻ�����������xh�������γ��ֱ����y1km��y2km�ĵط���ͼ�е��߶�OA������BCDE�ֱ��ʾy1��y2��x֮��ĺ�����ϵ��
�����ͽγ��ֱ�Ӽס�������ͬʱ��������ͬһ��·������У��γ�����2.4h����Ϣ��ֱ���������������ԭ�ٶȼ�����ʻ�����������xh�������γ��ֱ����y1km��y2km�ĵط���ͼ�е��߶�OA������BCDE�ֱ��ʾy1��y2��x֮��ĺ�����ϵ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com