解:(1)由题意可得:

=300,
整理得n
2+n-600=0,
(n+25)(n-24)=0,
∴n
1=-25,n
2=24,
∵n为正整数,
∴n=24;
答:300是前24行的点数之和;
(2)由题意可得:
2+4+6+…+2n=2(1+2+3+…+n)=2×

=n(n+1);
(3)依题意,得n(n+1)=600,
即n
2+n-600=0,
△=
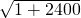
=
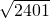
,无法开平方得出整数,
∴三角点阵中前n行的点数的和不能是600.
分析:(1)由于第一行有1个点,第二行有2个点…第n行有n个点…,则前五行共有(1+2+3+4+5)个点,前10行共有(1+2+3+4+5+6+7+8+9+10)个点,前n行共有(1+2+3+4+5+…+n)个点,然后求它们的和,前n行共有

个点,则

=300,然后解方程得到n的值;
(2)根据2+4+6+…+2n=2(1+2+3+…+n)=2×

进而得出即可;
(3)由(2)得n(n+1)=600,求n的值即可.
点评:此题主要考查了一元二次方程的应用以及规律型:图形的变化,本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

 如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点
如图有一个三角形点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点…第n行有n个点 =300,
=300, =n(n+1);
=n(n+1);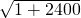 =
=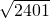 ,无法开平方得出整数,
,无法开平方得出整数, 个点,则
个点,则 =300,然后解方程得到n的值;
=300,然后解方程得到n的值; 进而得出即可;
进而得出即可;
