
【题目】如图,在△ABC中,BC的垂直平分线分别交BC、AC于点D、E,BE交AD于点F,AB=AD.
(1)判断△FDB与△ABC是否相似,并说明理由;
(2)BC=6,DE=2,求△BFD的面积.

【答案】(1)相似,理由见解析;(2)![]() .
.
【解析】
(1)根据线段垂直平分线的性质得出BE=CE,根据等腰三角形的性质得出∠EBC=∠ECB,∠ABC=∠ADB,根据相似三角形的判定得出即可;
(2)根据△FDB∽△ABC得出![]() =
=![]() =
=![]() ,求出AB=2FD,可得AD=2FD,DF=AF,根据三角形的面积得出S△AFB=S△BFD,S△AEF=S△EFD,根据DE为BC的垂直平分线可得S△BDE=S△CDE,可求出△ABC的面积,再根据相似三角形的性质求出答案即可.
,求出AB=2FD,可得AD=2FD,DF=AF,根据三角形的面积得出S△AFB=S△BFD,S△AEF=S△EFD,根据DE为BC的垂直平分线可得S△BDE=S△CDE,可求出△ABC的面积,再根据相似三角形的性质求出答案即可.
(1)△FDB与△ABC相似,理由如下:
∵DE是BC垂直平分线,
∴BE=CE,
∴∠EBC=∠ECB,
∵AB=AD,
∴∠ABC=∠ADB,
∴△FDB∽△ABC.
(2)∵△FDB∽△ABC,
∴![]() =
=![]() =
=![]() ,
,
∴AB=2FD,
∵AB=AD,
∴AD=2FD,
∴DF=AF,
∴S△AFB=S△BFD,S△AEF=S△EFD,
∴S△ABC=3S△BDE=3×![]() ×3×2=9,
×3×2=9,
∵△FDB∽△ABC,
∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,
,
∴S△BFD=![]() S△ABC=
S△ABC=![]() ×9=
×9=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动,与
上运动,与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的左侧),若点
的左侧),若点![]() 的横坐标的最小值为0,则点
的横坐标的最小值为0,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )
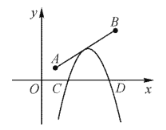
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校教学楼对面是一幢实验楼,小朱在教学楼的窗口C测得实验楼顶部D的仰角为20°,实验楼底部B的俯角为30°,量得教学楼与实验楼之间的距离AB=30m.求实验楼的高BD.(结果精确到1m.参考数据tan20°≈0.36,sin20°≈0.34,cos20°≈0.94,![]()
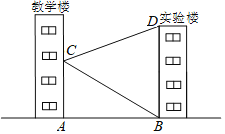
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F,且BE=DF.
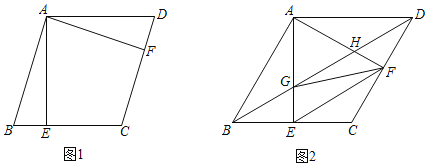
(1)如图1,求证:ABCD是菱形;
(2)如图2,连接BD,交AE于点G,交AF于点H,连接EF、FG,若∠CEF=30°,在不添加任何字母及辅助线的情况下,请直接写出图中面积是△BEG面积2倍的所有三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某鱼塘中养了某种鱼5000条,为了估计该鱼塘中该种鱼的总质量,从鱼塘中捕捞了3次,取得的数据如下:
数量/条 | 平均每条鱼的质量/kg | |
第1次捕捞 | 20 | 1.6 |
第2次捕捞 | 15 | 2.0 |
第3次捕捞 | 15 | 1.8 |
(1)求样本中平均每条鱼的质量;
(2)估计鱼塘中该种鱼的总质量;
(3)设该种鱼每千克的售价为14元,求出售该种鱼的收入y(元)与出售该种鱼的质量x(kg)之间的函数关系,并估计自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠BAC=45°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D.
(1)求证:BE=CF;
(2)当四边形ABDF为菱形时,求CD的长.
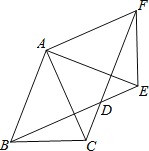
查看答案和解析>>
科目:初中数学 来源: 题型:
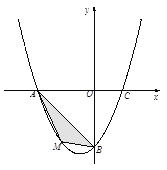
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com