解:(1)∵AB=2DE,AC=2DF,
∴
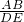
=

=2,
又由∠BAC=∠EDF,
∴△ABC∽△DEF(SAS),
∴

=2;
(2)由(1)知△ABC∽△DEF,
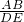
=

=2,
∴S
△ABC:S
△DEF=4:1,
∴S
△ABC=4S
△DEF,
又∵S
△DEF=2S
△DHF,S
△ABC=8,
∴S
△ABC=8S
△DHF=8,
∴S
△DHF=1.即△DHF的面积是1.

分析:(1)根据已知条件可以判定△ABC∽△DEF,然后由相似三角形的对应边成比例求得相似比是2,然后求得中线AG与DH的比;
(2)根据相似三角形的面积比等于相似比的平方求得△DEF的面积,然后利用△DEF与△DHF间的关系求△DHF的面积.
点评:本题考查了相似三角形的判定与性质.解得该题的关键是根据已知条件“AB=2DE,AC=2DF”求得△ABC和△DEF的对应边成比例,然后再由已知条件∠BAC=∠EDF证明△ABC∽△DEF.


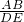 =
= =2,
=2, =2;
=2;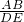 =
= =2,
=2,

