
 ��ͼ��ֱ��y=-x+3��x�ᣬy��ֱ��ཻ�ڵ�B��C������B��C�����������y=ax2+bx+c��x�����һ����ΪA������ΪP���ҶԳ�����ֱ��x=2��
��ͼ��ֱ��y=-x+3��x�ᣬy��ֱ��ཻ�ڵ�B��C������B��C�����������y=ax2+bx+c��x�����һ����ΪA������ΪP���ҶԳ�����ֱ��x=2������ ��1�������������ϵ��������������B��3��0����C��0��3�����ٸ��ݴ���ϵ�������������ߵĺ�������ʽ��
��2�����ڣ��������������B�㴹ֱBC��ֱ�ߵĽ���ʽΪy=x+b����C�㴹ֱBC��ֱ�߽���ʽΪy=x+3����BCΪб�ߣ��������ۿ����Q�����ꣻ
��3����M��x1��y1����N��x2��y2����T��a��b������T��PQ��x�ᣬ��M��N��MP��PQ��P��NQ��PQ��Q����֤��MPT�ס�TQN���������������ε����ʿɵ�a��x1+x2��-a2-x1x2=y1y2-b��y1+y2��+b2���ٸ���x1��x2��y1��y2��$\left\{\begin{array}{l}{y=kx+4}\\{y={x}^{2}-4x+3}\end{array}\right.$�Ľ⣬�õ�x2-��4+k��x-1=0���õ�kΪ�κ�ʵ����3-b=0��16-4b-a=0��a2-4a-8b+b2+15=0�����a=4��b=3���Ӷ���⣮
��� �⣺��1����ֱ��y=-x+3��x�ᣬy��ֱ��ཻ�ڵ�B��C��
��B��3��0����C��0��3����
�߶Գ���Ϊֱ��x=2��
����������ߵĺ�������ʽΪy=a��x-1����x-3����
��C��0��3�������3a=3�����a=1��
��������ߵĺ�������ʽy=��x-1����x-3��=x2-4x+3��
��2�����ڣ����B�㴹ֱBC��ֱ�ߵĽ���ʽΪy=x+b��
��B��3��0�������b=-3��
��ֱ�ߵĽ���ʽΪy=x-3��
��������$\left\{\begin{array}{l}{y=x-3}\\{y={x}^{2}-4x+3}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=-1}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=0}\end{array}\right.$��
��Q1��2��-1����
��C�㴹ֱBC��ֱ�߽���ʽΪy=x+3��
��������$\left\{\begin{array}{l}{y=x+3}\\{y={x}^{2}-4x+3}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=3}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=5}\\{{y}_{2}=8}\end{array}\right.$��
��Q2��5��8����
��BCΪб�ߣ���£�a��a2-4a+3������
a2+��a2-4a��2+��a-3��2+��a2-4a+3��2=18��
a3-8a2+20a-15=0��
��a-3����a2-5a+5��=0��
���a1=3��a2=$\frac{5��\sqrt{5}}{2}$��
��Q3��$\frac{5+\sqrt{5}}{2}$��$\frac{\sqrt{5}+1}{2}$����Q4��$\frac{5-\sqrt{5}}{2}$��$\frac{1-\sqrt{5}}{2}$����
����ڵ�Q��ʹ���Ե�B��C��QΪ�����������Ϊֱ�������Σ�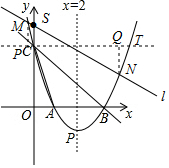 ��3����M��x1��y1����N��x2��y2����T��a��b����
��3����M��x1��y1����N��x2��y2����T��a��b����
��T��PQ��x�ᣬ��M��N��MP��PQ��P��NQ��PQ��Q��
���MTN=90�㣬
���MPT�ס�TQN��
��$\frac{{x}_{2}-a}{{y}_{1}-b}$=$\frac{{y}_{2}-b}{a-{x}_{1}}$��
a��x1+x2��-a2-x1x2=y1y2-b��y1+y2��+b2��
����x1��x2��y1��y2��$\left\{\begin{array}{l}{y=kx+4}\\{y={x}^{2}-4x+3}\end{array}\right.$�Ľ⣬
��x2-��4+k��x-1=0��
x1x2=-1��
x1+x2=k+4��
y1y2=k2x1x2+4k��x1+x2��+16=-k2+4k��k+4��+16��
y1+y2=k��k+4��+8��
1+a��k+4��-a2=-k2+4k��k+4��+16-b��k2+4k+8��+b2��
1+ak+4a-a2=-k3+4k2+16k+16-bk2-4bk-8b+b2��
�ࣨ3-b��k2+��16-4b-a��k+a2-4a-8b+b2+15=0��
��y=kx+b����������
��kΪ�κ�ʵ����3-b=0��16-4b-a=0��a2-4a-8b+b2+15=0��
���a=4��b=3��
���ڵ�T��4��3��ʹ�ò�������T������ֱ��l���С�MTN=90�㣮
���� ���⿼���˶��κ������ۺ����ͣ������漰����֪ʶ�������ô���ϵ������һ�κ����Ľ���ʽ�����κ����Ľ���ʽ��ֱ�������ε��ж������ʣ����������ε��ж������ʣ��ۺ��Խ�ǿ����һ���Ѷȣ��������ν�ϡ��������ۼ�����˼���ǽ���Ĺؼ���


 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
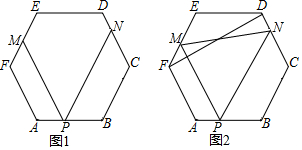 ����������ABCDEF�У�P��AB����һ�㣬PM��AF��EF��M��PN��BC��CD��N��
����������ABCDEF�У�P��AB����һ�㣬PM��AF��EF��M��PN��BC��CD��N���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}^{2}}{x+2}$=$\frac{4}{x+2}$ | B�� | $\sqrt{x-2}$+x=0 | C�� | x2-2=0 | D�� | x2+y2=1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com