Question

7．如图1，在四边形ABCD中，AD∥BC，∠B=90°，BC=m，AD=n，动点P从点B出发依次沿线段BA，AD，DC向点C移动，设移动路程为z，△BPC的面积S随着z的变化而变化的图象如图2所示，m，n是常数．
（1）写出线段AB和AD的长度．
（2）求m的值．
（3）当△APD是等腰三角形时，求s的值．

Answer 1

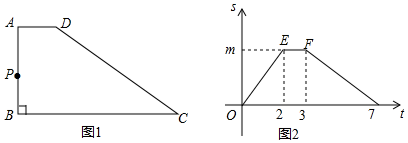
分析 （1）由点E的横坐标为2，可得AB=2，由点F的横坐标为3，可得AD=3-2=1；
（2）过D作DG⊥BC于G，则DG=AB=2，由图2可得，CD=7-3=4，在Rt△CDG中，根据勾股定理可得CG的长，进而得到BC=1+2$\sqrt{3}$，即m的值为1+2$\sqrt{3}$；
（3）分三种情况：①当点P在AB上时，若AP=AD=1，则△ADP是等腰三角形；②当点P在AD上时，△ADP不存在；③当点P在CD上时，若DP=DA=1，则△ADP是等腰三角形，分别根据点P的位置，运用三角形面积计算公式求得S的值．

解答 解：（1）由图可得，当点P在BA上移动时，△BPC的面积S随着z的增加而增加，
当点P与点A重合时，△BPC的面积最大，由点E的横坐标为2，可得AB=2，
当点P在AD上移动时，△BPC的面积不变，由点F的横坐标为3，可得AD=3-2=1，
故AB的长为2，AD的长为1；

（2）如图1，过D作DG⊥BC于G，则DG=AB=2，

由图2可得，CD=7-3=4，
∴Rt△CDG中，CG=$\sqrt{C{D}^{2}-D{G}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，
又∵BG=AD=1，
∴BC=1+2$\sqrt{3}$，
即m的值为1+2$\sqrt{3}$；

（3）分三种情况：
①当点P在AB上时，若AP=AD=1，则△ADP是等腰三角形，
此时，BP=2-1=1，
∴S=$\frac{1}{2}$BC×BP=$\frac{1}{2}$（1+2$\sqrt{3}$）×1=$\frac{1}{2}$+$\sqrt{3}$；
②当点P在AD上时，△ADP不存在；
③当点P在CD上时，若DP=DA=1，则△ADP是等腰三角形，
如图所示，过P作PG⊥BC于G，交AD的延长线于H，则矩形ABGH中，HG=AB=2，

∵AH∥BC，
∴△DPH∽△CPG，
∴$\frac{DP}{PC}$=$\frac{HP}{PG}$，即$\frac{1}{3}$=$\frac{2-GP}{GP}$，
解得GP=$\frac{3}{2}$，
∴S=$\frac{1}{2}$BC×GP=$\frac{1}{2}$（1+2$\sqrt{3}$）×$\frac{3}{2}$=$\frac{3}{4}$+$\frac{3}{2}$$\sqrt{3}$．

点评 本题属于四边形综合题，主要考查了直角梯形，矩形的性质，勾股定理以及相似三角形的运用，解决问题的关键是作辅助线构造矩形，运用分类思想进行求解，解题时注意：矩形的对边相等，相似三角形的对应边成比例．