
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{5}$或5 | C. | 2$\sqrt{6}$ | D. | 5 |
分析 分两种情形:①当高AD在△ABC内时.②当高AD在△ACB′外时.分别求解即可.
解答 解:如图①当高AD在△ABC内时,由题意EA=EB=AC=2$\sqrt{5}$.
②当高AD在△ACB′外时,设AB′=B′E=x.
在Rt△ADC中,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{(2\sqrt{5})^{2}-{4}^{2}}$=2,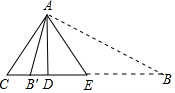
由题意DE=DC=2,
在Rt△AED中,∵AB′2=AD2+DB′2,
∴x2=42+(x-2)2,
∴x=5.
∴线段BE的长度为2$\sqrt{5}$或5,
故选B.
点评 本题考查翻折变换、等腰三角形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,出现高的问题,注意高在三角形内和三角形外两种情形,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 5,7 | B. | 6,7 | C. | 8,6 | D. | 8,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
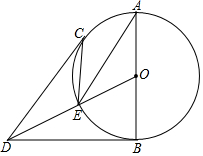 如图,AB是⊙O的直径,DB,DC分别与⊙O相切于B,C,OD交⊙O于点E,
如图,AB是⊙O的直径,DB,DC分别与⊙O相切于B,C,OD交⊙O于点E,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
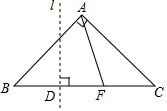 如图,等腰Rt△ABC中,AB=AC=1,点F是边BC上不与点B、C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$.
如图,等腰Rt△ABC中,AB=AC=1,点F是边BC上不与点B、C重合的一个动点,直线l垂直平分BF,垂足为D,当△AFC是等腰三角形时,BD的长为$\frac{\sqrt{2}}{4}$或$\frac{\sqrt{2}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
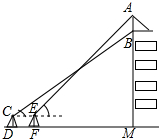 小华周末去汉唐书城买书,发现书城所在的大楼的楼顶有一面大约3m高的旗帜(如图所示),于是他想利用所学知识测量下书城所在大楼的高度,小华在楼前空地上的点D处,用1.3米高的测角仪CD从点C测得旗帜的底部B的仰角为35°,然后向教学楼正方向走了5米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.已知点A、B、M在同一直线上,CD⊥DM,EF⊥DM,请根据以上数据,求这座大楼的高度BM.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.结果精确到0.1m).
小华周末去汉唐书城买书,发现书城所在的大楼的楼顶有一面大约3m高的旗帜(如图所示),于是他想利用所学知识测量下书城所在大楼的高度,小华在楼前空地上的点D处,用1.3米高的测角仪CD从点C测得旗帜的底部B的仰角为35°,然后向教学楼正方向走了5米到达点F处,又从点E测得旗帜的顶部A的仰角为45°.已知点A、B、M在同一直线上,CD⊥DM,EF⊥DM,请根据以上数据,求这座大楼的高度BM.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70.结果精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com