练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知一次函数y=kx+b的图象经过点（-2，-4），且与正比例函数y＝x的图象相交于点（4，a），求：
    （1）a的值；
    （2）k、b的值；
    （3）这两个函数的图象与y轴相交得到的三角形的面积．

    （1）2；（2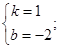）（3）4.

    解析试题分析：（1）要求的a值，就需要把点（4，a）代入正比例函数y＝x中即可以求得a的值；（2）要求出字母k,b的值，就需要把点（-2，-4），点（4，a），代入一次函数y=kx+b中即可得k，b的值；（3）根据根据求出的两个函数图象，画出相关喊出图像即可得到图形，与它们与y轴相交得到的三角形的面积等于（2）得到的直线与y轴的交点的绝对值与两直线交点的横坐标的积的一半．
    试题解析：（1）（1）将点（4，a）代入正比例函数y＝x，
    解得a=2；
    (2)将点（4,2）、（-2，-4）分别代入y=kx+b得：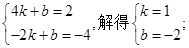

    （3）画出图形如下：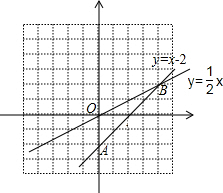

    直线y=x-2交y轴于点（0，-2），∴围成的三角形的面积为×2×4=4．
    考点：两条直线相交或平行问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2008年5月12日14时28分四川汶川发生里氏8.0级强力地震．某市接到上级通知，立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区．乙组由于要携带一些救灾物资，比甲组迟出发1.25小时（从甲组出发时开始计时）．图中的折线、线段分别表示甲、乙两组的所走路程y甲（千米）、y乙（千米）与时间x（小时）之间的函数关系对应的图象．请根据图象所提供的信息，解决下列问题：

    （1）由于汽车发生故障，甲组在途中停留了              小时；
    （2）甲组的汽车排除故障后，立即提速赶往灾区．请问甲组的汽车在排除故障时，距出发点的路程是多少千米？
    （3）为了保证及时联络，甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米，请通过计算说明，按图象所表示的走法是否符合约定？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某蔬菜经销商到蔬菜种植基地采购一种蔬菜，经销商一次性采购蔬菜的采购单价y（元/千克）与采购量x（千克）之间的函数关系图象如图中折线AB——BC——CD所示（不包括端点A）．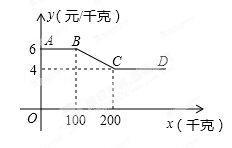

    （1）当100＜x＜200时，直接写y与x之间的函数关系式．
    （2）蔬菜的种植成本为2元/千克，某经销商一次性采购蔬菜的采购量不超过200千克，当采购量是多少时，蔬菜种植基地获利最大，最大利润是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知反比例函数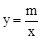（m是常数，m≠0），一次函数y＝ax＋b（a、b为常数，a≠0），其中一次函数与x轴，y轴的交点分别是A（－4，0），B（0，2）．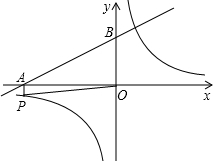

    （1）求一次函数的关系式；
    （2）反比例函数图象上有一点P满足：①PA⊥x轴；②PO＝（O为坐标原点），求反比例函数的关系式；
    （3）求点P关于原点的对称点Q的坐标，判断点Q是否在该反比例函数的图象上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    “母亲节”到了，八年级（1）班班委发起慰问烈属王大妈的活动，决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集慰问金．已知同学们从花店按每支1.2元买进鲜花，并按每支3元卖出．
    （1）求同学们卖出鲜花的销售额（元）与销售量（支）之间的函数关系式；
    （2）若从花店购买鲜花的同时，还总共用去40元购买包装材料，求所筹集的慰问金（元）与销售量（支）之间的函数关系式；若要筹集不少于500元的慰问金，则至少要卖出鲜花多少支？（慰问金=销售额－成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行，并以各自的速度匀速行驶，途径配货站C，甲车先到达C地，并在C地用1小时配货，然后按原速度开往B地，乙车从B地直达A地，下图是甲、乙两车间的距离（千米）与乙车出发（时）的函数的部分图像.

    （1）A、B两地的距离是          千米，乙车出发         小时与甲相遇；
    （2）求乙车出发1.5小时后直至到达A地的过程中，与的函数关系式及的取值范围；
    （3）乙车出发多长时间，两车相距100千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    点P（x，y）在第一象限，且x+y=10，点A的坐标为（8，0），设原点为O，△OPA的面积为S．
    （1）求S与x的函数关系式，写出x的取值范围，画出这个函数图象；
    （2）当S=12时，求点P的坐标；
    （3）△OPA的面积能大于40吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，已知直线：、直线：，直线、分别交x轴于B、C两点，、相交于点A．

    （1）求A、B、C三点坐标；
    （2）求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知一次函数的图象与反比例函数的图象相交，其中一个交点的纵坐标为6．
    （1）求两个函数的解析式；
    （2）若已知另一点的横坐标为，结合图象求出时ｘ的取值范围．

    查看答案和解析>>

    同步练习册答案