
【题目】如图(1) ,折叠平行四边形![]() ,使得
,使得![]() 分别落在
分别落在![]() 边上的
边上的![]() 点,
点,![]() 为折痕
为折痕

(1)若![]() ,证明:平行四边形
,证明:平行四边形![]() 是菱形;
是菱形;
(2)若![]() ,求
,求![]() 的大小;
的大小;
(3)如图(2) ,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,若
,若![]() ,求
,求![]() 的大小
的大小
【答案】(1)详见解析;(2)30°;(3)45°.
【解析】
(1)利用面积法解决问题即可.
(2)分别求出∠BAD,∠BAB′,∠DAD′即可解决问题.
(3)如图2中,延长AE到H,使得EH=EA,连接CH,HG,EF,AC.想办法证明E,H,G,C四点共圆,可得∠EGC=∠EHC=45°.
(1)证明:如图1中,
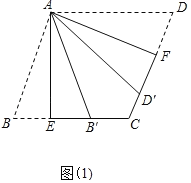
∵四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,
∴S平行四边形ABCD=BCAE=CDAF,
∵AE=AF,
∴BC=CD,
∴平行四边形![]() 是菱形;
是菱形;
(2)解:如图1中,
∵四边形ABCD是平行四边形,
∴∠C=∠BAD=110°,
∵AB∥CD,
∴∠C+∠B=180°,
∴∠B=∠D=70°,
∵AE⊥BC,AF⊥CD.
∴∠AEB=∠AFD=90°,
∴∠BAE=∠DAF=20°,
由翻折变换的性质可知:∠BAB′=2∠BAE=40°,∠DAD′=2∠DAF=40°,
∴∠B′AD′=110°﹣80°=30°.
(3)解:如图2中,延长AE到H,使得EH=EA,连接CH,HG,EF,AC.

∵EA=EC,∠AEC=90°,
∴∠ACE=45°,
∵∠AEC+∠AFC=180°,
∴A,B,C,F四点共圆,
∴∠AFE=∠ACE=45°,
∵四边形AEGF是平行四边形,
∴AF∥EG,AE=FG,
∴∠AFE=∠FEG=45°,
∴EH=AE=FG,EH∥FG,
∴四边形EHGF是平行四边形,
∴EF∥HG,
∴∠FEG=∠EGH=45°
∵EC=AE=EH,∠CEH=90°,
∴∠ECH=∠EHC=45°,
∴∠ECH=∠EGH,
∴E,H,G,C四点共圆,∠EGC=∠EHC=45°.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
①图2中的阴影部分的面积为 ;
②观察图2请你写出 (a+b)2、(a﹣b)2、ab之间的等量关系是 ;
③根据(2)中的结论,若x+y=5,xy=![]() ,则(x﹣y)2= ;
,则(x﹣y)2= ;
④实际上通过计算图形的面积可以探求相应的等式.
如图3,你发现的等式是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,某地准备开荒种树,两次参加活动的人数及开支如下表:
开荒(人) | 种树(人) | 总支出(元) | |
第一次 | 15 | 9 | 57000 |
第二次 | 10 | 16 | 68000 |
(1)若两次开荒种树活动的人均支出费用一样,求开荒和种树的人均支出费用各是多少?
(2)在人均支出费用不变的情况下,为节约开支,施工单位准备抽调40人参加此活动,要使得总支出不超过102 000元,且开荒人数小于种树人数,则有哪几种分配人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
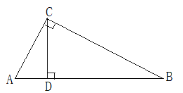
【题目】如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.
(1)求△ABC的面积;
(2)求CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC上的高DF,当BD=![]() 时,试求出DF的长(用
时,试求出DF的长(用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线![]() 与直线
与直线![]() 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线![]() 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线![]() 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com