
【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 上的一点,
上的一点,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .若
.若![]() 是
是![]() 的中点,则
的中点,则![]() 的长是________.
的长是________.

【答案】10.5
【解析】
根据线段中点的定义可得CG=DG,然后利用“角边角”证明△DEG和△CFG全等,根据全等三角形对应边相等可得DE=CF,EG=FG,设DE=x,表示出BF,再利用勾股定理列式求EG,然后表示出EF,再根据线段垂直平分线上的点到两端点的距离相等可得BF=EF,然后列出方程求出x的值,从而求出AD,再根据矩形的对边相等可得BC=AD.
∵矩形ABCD中,G是CD的中点,AB=12,
∴CG=DG=![]() CD=
CD=![]() AB =
AB =![]() ×12=6,
×12=6,
在△DEG和△CFG中,
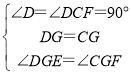 ,
,
∴△DEG≌△CFG(ASA),
∴DE=CF,EG=FG,
设DE=![]() ,
,
则BF=BC+CF=AD+CF=![]() ,
,
在Rt△DEG中,
EG=![]() ,
,
∴EF=2 EG=2![]() ,
,
∵FH垂直平分BE,
∴BF=EF,
∴![]() 2
2![]() ,
,
解得![]() ,
,
∴AD=AE+DE![]() ,
,
∴BC=AD=10.5.
故答案为:10.5.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
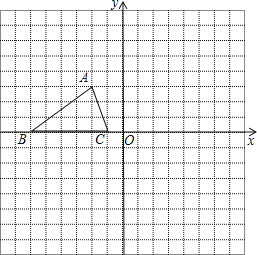
(1)请直接写出点A关于y轴对称的点的坐标为 ;
(2)将△ABC平移,使点B移动后的坐标为B′(﹣5,﹣5),画出平移后的图形△A′B′C′;
(3)将△ABC绕坐标原点O顺时针旋转90°,画出旋转后的图形△A″B″C″.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=![]() S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.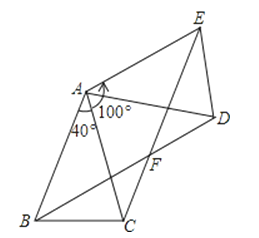
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“每天在校体育活动时间”的问题随机抽样调查了321名初中学生.根据调查结果将学生每天在校体育活动时间t(小时)分成![]() ,
,![]() ,
,![]() ,
,![]() 四组,并绘制了统计图(部分).
四组,并绘制了统计图(部分).
![]() 组:
组:![]() 组:
组:![]() 组:
组:![]() 组:
组:![]()

请根据上述信息解答下列问题:
(1)![]() 组的人数是 ;
组的人数是 ;
(2)本次调查数据的中位数落在 组内;
(3)若该市约有12840名初中学生,请你估算其中达到国家规定体育活动时间的人数大约有多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建小区要在一块等边三角形内修建一个圆形花坛.
(1)要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(2)若这个等边三角形的周长为36米,请计算出花坛的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请用两种不同的方法列代数式表示图中阴影部分的面积.

方法①_________________;
方法②_________________;
(2)根据(1)写出一个等式________________;
(3)若![]() ,
,![]() .
.
①求![]() 的值。
的值。
②![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC. (Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DFDA.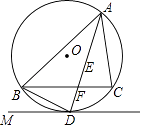
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com