
【题目】如图,已知等腰△ABC顶角∠A=36°.
(1)尺规作图:在AC上作一点D,使AD=BD;(保留作图痕迹,不必写作法和证明)
(2)求证:△BCD是等腰三角形.

【答案】(1)见解析;(2)△BCD是等腰三角形
【解析】
(1)根据垂直平分线的尺规作图方法,作AB的垂直平分线交AC于点D,点D即为所求.
(2)已知等腰△ABC顶角∠A=36°,![]() ,再证明∠BDC=72°,即可证明△BCD是等腰三角形.
,再证明∠BDC=72°,即可证明△BCD是等腰三角形.
(1)如图1,作AB的垂直平分线,分别以点A、B为圆心,以大于![]() 为半径在AB上方画弧,在AB上方两圆弧交点为点M,分别以点A、B为圆心以大于
为半径在AB上方画弧,在AB上方两圆弧交点为点M,分别以点A、B为圆心以大于![]() 为半径在AB下方画弧,在AB下方两圆弧交点为点N.过点M、N作直线MN,交AC于点D,点D即为所求.
为半径在AB下方画弧,在AB下方两圆弧交点为点N.过点M、N作直线MN,交AC于点D,点D即为所求.
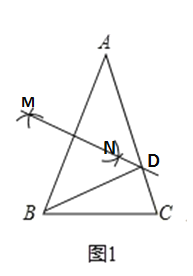
(2)∵在等腰△ABC顶角∠A=36°
∴![]()
∵AD=BD
∴∠ABD=∠A=36°
则∠DBC=36°
在△BCD中∠ACB=72°
∠DBC=36°
∠BDC=72°=∠ACB
∴△BCD是等腰三角形


科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点A、B的坐标是(a,0)(b,0),a,b满足方程组![]() ,C为y轴正半轴上一点,且S△ABC=6.
,C为y轴正半轴上一点,且S△ABC=6.
(1)求A、B、C三点的坐标;
(2)是否存在点P(t,t),使S△PAB=![]() S△ABC?若存在,请求出P点坐标;若不存在,请说明理由;
S△ABC?若存在,请求出P点坐标;若不存在,请说明理由;
(3)若点C沿y轴负半轴方向以每秒1个单位长度平移至点D,当运动时间t为多少秒时,四边形ABCD的面积S为15个平方单位?求出此时点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“构造图形解题”,它的应用十分广泛,特别是有些技巧性很强的题目,如果不能发现题目中所隐含的几何意义,而用通常的代数方法去思考,经常让我们手足无措,难以下手,这时,如果能转换思维,发现题目中隐含的几何条件,通过构造适合的几何图形,将会得到事半功倍的效果,下面介绍两则实例:
实例一:1876年,美国总统伽非尔德利用实例一图证明了勾股定理:由
S四边形ABCD=S△ABC+S△ADE+S△ABE得![]() ,化简得:
,化简得:![]()
实例二:欧几里得的《几何原本》记载,关于x的方程![]() 的图解法是:
的图解法是:
画Rt△ABC,使∠ABC=90°,BC=![]() ,AC=
,AC=![]() ,再在斜边AB上截取BD=
,再在斜边AB上截取BD=![]() ,则AD的长就是该方程的一个正根(如实例二图)
,则AD的长就是该方程的一个正根(如实例二图)
请根据以上阅读材料回答下面的问题:
(1)如图1,请利用图形中面积的等量关系,写出甲图要证明的数学公式是 ,乙图要证明的数学公式是
(2)如图2,若2和-8是关于x的方程x2+6x=16的两个根,按照实例二的方式构造Rt△ABC,连接CD,求CD的长;
(3)若x,y,z都为正数,且x2+y2=z2,请用构造图形的方法求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
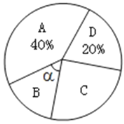
【题目】2019年10月,某市高质量通过全国文明城市测评,该成绩的取得得益于领导高度重视(A)、整改措施有效(B)、市民积极参与(C)、市民文明素质(D).某数学兴趣小组随机走访了部分市民,对这四项认可度进行调查(只选填最认可的一项),并将调查结果制作了如下两幅不完整的统计图.
(1)请补全D项的条形图;
(2)已知B、C两项条形图的高度之比为3:5.
①选B、C两项的人数各为多少个?
②求α的度数,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在面积为3的△ABC中,AB=3,∠BAC=45°,点D是BC边上一点.
(1)若AD是BC边上的中线,求AD的长;
(2)点D关于直线AB和AC的对称点分别为点M、N,求AN的长度的最小值;
(3)若P是△ABC内的一点,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
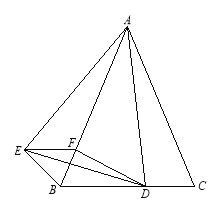
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com