
【题目】为鼓励返乡农民工创业,宿州市政府制定了小型企业的优惠政策,许多小型企业应运而生.某镇统计了该镇今年1~5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图:
今年1~5月各月新注册小型企业今年1~5月各月新注册小型企业数量占今年前数量折线统计图五月新注册小型企业总量的百分比扇形统计图
(1)某镇今年1~5月新注册小型企业一共有 家,请将折线统计图补充完整.
(2)该镇今年3月新注册的小型企业中,只有2家是餐饮企业.现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
【答案】(1)16(2)![]()
【解析】试题分析:(1)根据3月份有4家,占25%,可求出某镇今年1-5月新注册小型企业一共有的家数,再求出1月份的家数,进而将折线统计图补充完整.(2)设该镇今年3月新注册的小型企业为甲、乙、丙、丁,其中甲、乙为餐饮企业,根据题意画出树状图,然后由树状图求得所有等可能的结果与甲、乙2家企业恰好被抽到的情况,再利用概率公式求解即可求得答案.
试题解析:
(1)根据统计图可知,3月份有4家,占25%,
所以某镇今年1﹣5月新注册小型企业一共有:4÷25%=16(家),
1月份有:16﹣2﹣4﹣3﹣2=5(家).
折线统计图补充如下:

故答案为:16;
(2)设该镇今年3月新注册的小型企业为甲、乙、丙、丁,其中甲、乙为餐饮企业.画树状图得:
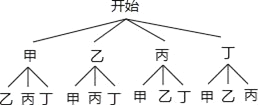
∵共有12种等可能的结果,甲、乙2家企业恰好被抽到的有2种,
∴所抽取的2家企业恰好都是餐饮企业的概率为![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们规定:有理数![]() 用数轴上点
用数轴上点![]() 表示,
表示,![]() 叫做点
叫做点![]() 在数轴上的坐标;有理数
在数轴上的坐标;有理数![]() 用数轴上点
用数轴上点![]() 表示,
表示,![]() 叫做点
叫做点![]() 在数轴上的坐标.
在数轴上的坐标.![]() 表示数轴上的两点
表示数轴上的两点![]() ,
,![]() 之间的距离.
之间的距离.
(1)借助数轴,完成下表:
|
|
|
|
3 | 2 | 1 | 1 |
1 | 5 | ______ | ______ |
2 | -3 | ______ | ______ |
-4 | 1 | ______ | ______ |
-5 | -2 | ______ | ______ |
-3 | -6 | ______ | ______ |
(2)观察(1)中的表格内容,猜想![]() ______;(用含
______;(用含![]() ,
,![]() 的式子表示,不用说理)
的式子表示,不用说理)
(3)已知点![]() 在数轴上的坐标是-2,且
在数轴上的坐标是-2,且![]() ,利用(2)中的结论求点
,利用(2)中的结论求点![]() 在数轴上的坐标.
在数轴上的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
表示两人离A地的距离S(km)与时间t(h)的关系,结合图像回答下列问题:
(1)表示乙离开A地的距离与时间关系的图像是________(填![]() );
);
甲的速度是__________km/h;乙的速度是________km/h。
(2)甲出发后多少时间两人恰好相距5km?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合),以AD为边在AD的右侧作正方形ADEF,连接CF.
(1)观察猜想:如图(1),当点D在线段BC上时,
①BC与CF的位置关系是: ;
②BC、CD、CF之间的数量关系为: (将结论直接写在横线上)
(2)数学思考:如图(2),当点D在线段CB的延长线上时,上述①、②中的结论是否仍然成立?若成立,请给予证明,若不成立,请你写出正确结论再给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示).
![]()
左右折叠纸面,折痕所在的直线与数轴的交点为“对折中心点”
操作一:
(1)左右折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与 表示的点重合;
操作二:
(2)左右折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①对折中心点所表示的数为 ,对折后5表示的点与数 表示的点重合;
②若数轴上A.B两点之间距离为11(A在B的左侧),且A.B两点经折叠后重合,求A.B两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市质量技术监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:

(1)若标准质量为450克,则抽样检测的20袋食品的总质量为多少克?
(2)若该种食品的合格标准为450±5g,求该食品的抽样检测的合格率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,CD是弦,且AB![]() CD于点E。连接AC、OC、BC。
CD于点E。连接AC、OC、BC。
(1)求证: ![]() ACO=
ACO=![]() BCD。
BCD。
(2)若EB=![]() ,CD=
,CD=![]() ,求⊙O的直径。
,求⊙O的直径。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是8×6的网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:
(1)在图1中画一个以线段AB为一边周长为10+2![]() 的平行四边形,所画图形的各顶点必须在小正方形的顶点上.
的平行四边形,所画图形的各顶点必须在小正方形的顶点上.
(2)在图2中画一个以线段AB为一边的等腰三角形,所画等腰三角形的各顶点必须在小正方形的顶点上,并求出该等腰三角形的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
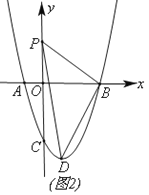
【题目】如图,在平面直角坐标中,抛物线y=ax2-2ax-3a(a≠0)与x轴交于A、B(A在B的左侧),与y轴交于点C,且OC=3OA.
(1)如图(1)求抛物线的解析式;
(2)如图(2)动点P从点O出发,沿y轴正方向以每秒1个单位的速度移动,点D是抛物线顶点,连接PB、PD、BD,设点P运动时间为t(单位:秒),△PBD的面积为S,求S与t的函数关系式;
(3)如图(3)在(2)的条件下,延长BP交抛物线于点Q,过点O作OE⊥BQ,垂足为E,连接CE、CB,若CE=CB,求t值,并求出此时的Q点坐标.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com