
分析 (1)设乙种客车的单车载客量为x,则甲种客车的单车载客量是$\frac{3}{4}$x,根据租用甲种客车辆数=租用乙种客车辆数+1,列方程求解,结果要检验;
(2)设租用甲种客车a辆,则需租用乙种客车(6-a)辆,由租用乙种客车数量不少于租用甲种客车数量列不等式求得a的范围,继而根据总费用=甲车的租车费用+乙车的租车费用列出函数解析式,结合a的范围可得其最值情况.
解答 解:(1)设乙种客车的单车载客量为x,则甲种客车的单车载客量是$\frac{3}{4}$x,
根据题意,得:$\frac{270}{\frac{3}{4}x}$=$\frac{270+30}{x}$+1,
解得:x=60,
经检验x=60是原分式方程的解,
$\frac{270}{60}$=4.5,
∴本次旅游若只租用乙种客车乘载这270名师生,应租5辆;
(2)设租用甲种客车a辆,则需租用乙种客车(6-a)辆,
∴6-a≥a,
解得:a≤3,
令租车总费用为W,
则W=250a+300(6-a)=-50a+1800,
∵W随a的增大而减小,
∴当a=3时,W取得最大值,最大值为-50×3+1800=1650(元),
答:当租用甲种客车3辆、乙种客车3辆,租车费用最少,为1650元.
点评 本题主要考查分式方程的应用及一次函数的应用,理解题意找到题目中蕴含的相等关系是解题的关键.


科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:判断题
已知,A,B 两市相距 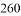 千米,甲车从 A 市前往 B 市运送物资,行驶
千米,甲车从 A 市前往 B 市运送物资,行驶  小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过
小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过  分钟修好甲车后以原速原路返回,同时甲车以原速
分钟修好甲车后以原速原路返回,同时甲车以原速 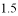 倍的速度前往 B 市,如图是两车距 A 市的路程
倍的速度前往 B 市,如图是两车距 A 市的路程  (千米)与甲车行驶时间
(千米)与甲车行驶时间  (小时)之间的函数图象,结合图象回答下列问题:
(小时)之间的函数图象,结合图象回答下列问题:
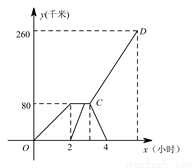
(1)直接写出甲车提速后的速度、乙车的速度、点  的坐标;
的坐标;
(2)求乙车返回时  与
与  的函数关系式并直接写出自变量
的函数关系式并直接写出自变量  的取值范围;
的取值范围;
(3)求甲车到达 B 市时乙车已返回 A 市多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25cm | B. | 35cm | C. | 30cm | D. | 40cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.
如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com