
ЁОЬтФПЁПЕШбќRtЁїACBЃЌЁЯACBЃН90ЁуЃЌACЃНBCЃЌЕуAЁЂCЗжБ№дкxжсЁЂyжсЕФе§АыжсЩЯЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКЁЯBCOЃНЁЯCAO
ЃЈ2ЃЉШчЭМ2ЃЌШєOAЃН5ЃЌOCЃН2ЃЌЧѓBЕуЕФзјБъ
ЃЈ3ЃЉШчЭМ3ЃЌЕуCЃЈ0ЃЌ3ЃЉЃЌQЁЂAСНЕуОљдкxжсЩЯЃЌЧвSЁїCQAЃН18ЃЎЗжБ№вдACЁЂCQЮЊбќдкЕквЛЁЂЕкЖўЯѓЯозїЕШбќRtЁїCANЁЂЕШбќRtЁїQCMЃЌСЌНгMNНЛyжсгкPЕуЃЌOPЕФГЄЖШЪЧЗёЗЂЩњИФБфЃПШєВЛБфЃЌЧѓГіOPЕФжЕЃЛШєБфЛЏЃЌЧѓOPЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉЃЈЉ2ЃЌЉ3ЃЉЃЈ3ЃЉOPЕФГЄЖШВЛЛсЗЂЩњИФБфЃЌ9
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭЌНЧЕФгрНЧЯрЕШЕУГіНсТлМДПЩЃЛ
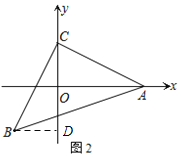
ЃЈ2ЃЉЯШЙ§ЕуBзїBDЁЭyжсгкDЃЌдйХаЖЈЁїCDBЁеЁїAOCЃЈAASЃЉЃЌЧѓЕУBD=CO=2ЃЌCD=AO=5ЃЌНјЖјЕУГіOD=5-2=3ЃЌМДПЩЕУЕНBЕуЕФзјБъЃЛ
ЃЈ3ЃЉЯШЙ§NзїNHЁЮCMЃЌНЛyжсгкHЃЌдйЁїHCNЁеЁїQACЃЈASAЃЉЃЌЕУГіCH=AQЃЌHN=QCЃЌШЛКѓИљОнЕуCЃЈ0ЃЌ3ЃЉЃЌSЁїCQA=18ЃЌЧѓЕУAQ=12ЃЌзюКѓХаЖЈЁїPNHЁеЁїPMCЃЈAASЃЉЃЌЕУГі![]() ЃЌМДПЩЧѓЕУCP=3+6=9ЃЈЖЈжЕЃЉЃЎ
ЃЌМДПЩЧѓЕУCP=3+6=9ЃЈЖЈжЕЃЉЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌ
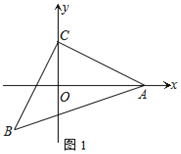
ЁпЁЯACBЃН90ЁуЃЌЁЯAOCЃН90ЁуЃЌ
ЁрЁЯBCO+ЁЯACOЃН90ЁуЃНЁЯCAO+ЁЯACOЃЌ
ЁрЁЯBCOЃНЁЯCAOЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЙ§ЕуBзїBDЁЭyжсгкDЃЌдђЁЯCDBЃНЁЯAOCЃН90ЁуЃЌ
дкЁїCDBКЭЁїAOCжаЃЌ
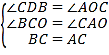 ЃЌ
ЃЌ
ЁрЁїCDBЁеЁїAOCЃЈAASЃЉЃЌ
ЁрBDЃНCOЃН2ЃЌCDЃНAOЃН5ЃЌ
ЁрODЃН5Љ2ЃН3ЃЌ
гжЁпЕуBдкЕкШ§ЯѓЯоЃЌ
ЁрBЃЈЉ2ЃЌЉ3ЃЉЃЛ
ЃЈ3ЃЉOPЕФГЄЖШВЛЛсЗЂЩњИФБфЃЎ
РэгЩЃКШчЭМ3ЃЌЙ§NзїNHЁЮCMЃЌНЛyжсгкHЃЌдђ
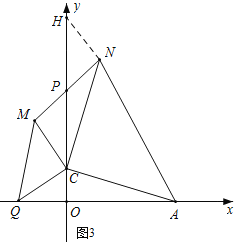
ЁЯCNH+ЁЯMCNЃН180ЁуЃЌ
ЁпЕШбќRtЁїCANЁЂЕШбќRtЁїQCMЃЌ
ЁрЁЯMCQ+ЁЯACNЃН180ЁуЃЌ
ЁрЁЯACQ+ЁЯMCNЃН360ЁуЉ180ЁуЃН180ЁуЃЌ
ЁрЁЯCNHЃНЁЯACQЃЌ
гжЁпЁЯHCN+ЁЯACOЃН90ЁуЃНЁЯQAC+ЁЯACOЃЌ
ЁрЁЯHCNЃНЁЯQACЃЌ
дкЁїHCNКЭЁїQACжаЃЌ
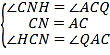 ЃЌ
ЃЌ
ЁрЁїHCNЁеЁїQACЃЈASAЃЉЃЌ
ЁрCHЃНAQЃЌHNЃНQCЃЌ
ЁпQCЃНMCЃЌ
ЁрHNЃНCMЃЌ
ЁпЕуCЃЈ0ЃЌ3ЃЉЃЌSЁїCQAЃН18ЃЌ
Ёр![]() ЁСAQЁСCOЃН18ЃЌМД
ЁСAQЁСCOЃН18ЃЌМД![]() ЁСAQЁС3ЃН18ЃЌ
ЁСAQЁС3ЃН18ЃЌ
ЁрAQЃН12ЃЌ
ЁрCHЃН12ЃЌ
ЁпNHЁЮCMЃЌ
ЁрЁЯPNHЃНЁЯPMCЃЌ
ЁрдкЁїPNHКЭЁїPMCжаЃЌ
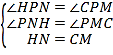 ЃЌ
ЃЌ
ЁрЁїPNHЁеЁїPMCЃЈAASЃЉЃЌ
ЁрCPЃНPHЃН![]() CHЃН6ЃЌ
CHЃН6ЃЌ
гжЁпCOЃН3ЃЌ
ЁрCPЃН3+6ЃН9ЃЈЖЈжЕЃЉЃЌ
МДOPЕФГЄЖШЪМжеЪЧ9ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDЕФЖдНЧЯпНЛгкЕуOЃЌЧвABЁйADЃЌЙ§OзїOEЁЭBDНЛBDгкЕуEЃЎШєЁїCDEЕФжмГЄЮЊ10ЃЌдђЦНааЫФБпаЮABCDЕФжмГЄЮЊЃЈ ЃЉ
A.10
B.16
C.18
D.20
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКгУ3СОAаЭГЕКЭ2СОBаЭГЕдиТњЛѕЮявЛДЮПЩдЫЛѕ17ЖжЃЛгУ2СОAаЭГЕКЭ3СОBаЭГЕдиТњЛѕЮявЛДЮПЩдЫЛѕl8ЖжЃЌФГЮяСїЙЋПЏЯжга35ЖжЛѕЮяЃЌМЦЛЎЭЌЪБзтгУAаЭГЕaСОЃЌBаЭГЕbСОЃЌвЛДЮдЫЭъЃЌЧвЧЁКУУПСОГЕЖМдиТњЛѕЮяЃЎ
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
(1)lСОAаЭГЕКЭlСОBаЭГЕЖМдиТњЛѕЮявЛДЮПЩЗжБ№дЫЛѕЖрЩйЖжЃП
(2)ЧыФуАяИУЮяСїЙЋЫОЩшМЦзтГЕЗНАИЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЃЌЧвТњзуЪНзг
ЃЌЧвТњзуЪНзг![]() .
.
ЃЈ1ЃЉЧѓГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЂйдк![]() жсЕФе§АыжсЩЯДцдквЛЕу
жсЕФе§АыжсЩЯДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЕФУцЛ§ЕФвЛАыЃЌЧѓГіЕу
ЕФУцЛ§ЕФвЛАыЃЌЧѓГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкдкзјБъжсЕФЦфЫќЮЛжУЪЧЗёДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФУцЛ§ЕШгк
ЕФУцЛ§ЕШгк![]() ЕФУцЛ§ЕФвЛАыШдШЛГЩСЂЃЌШєДцдкЃЌжБНгаДГіЦфЫћЗћКЯЬѕМўЕФЕу
ЕФУцЛ§ЕФвЛАыШдШЛГЩСЂЃЌШєДцдкЃЌжБНгаДГіЦфЫћЗћКЯЬѕМўЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЙ§Еу![]() зї
зї![]() жсНЛ
жсНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() бгГЄЯпЩЯвЛЖЏЕуЃЌСЌНг
бгГЄЯпЩЯвЛЖЏЕуЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дЫЖЏЪБЃЌЧѓжЄЃК
дЫЖЏЪБЃЌЧѓжЄЃК![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЕФБпГЄЪЧ4ЃЌ
ЕФБпГЄЪЧ4ЃЌ![]() ЕФЦНЗжЯпНЛ
ЕФЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌШєЕу
ЃЌШєЕу![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() КЭ
КЭ![]() ЩЯЕФЖЏЕуЃЌдђ
ЩЯЕФЖЏЕуЃЌдђ![]() ЕФзюаЁжЕЪЧ__________ЃЎ
ЕФзюаЁжЕЪЧ__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() Й§
Й§![]() ЕуЃЌЧвгы
ЕуЃЌЧвгы![]() жсНЛгк
жсНЛгк![]() ЕуЃЎ
ЕуЃЎ
ЃЈ1ЃЉЧѓЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЪдЫЕУїЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌдк
ЩЯЕФвЛИіЖЏЕуЃЌдк![]() жсЩЯЪЧЗёДцдкСэвЛИіЕу
жсЩЯЪЧЗёДцдкСэвЛИіЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDжаЃЌвбжЊЁЯBAD=120ЁуЃЌЁЯEGF=60Ёу, ЁЯEGFЕФЖЅЕуGдкСтаЮЖдНЧЯпACЩЯдЫЖЏЃЌНЧЕФСНБпЗжБ№НЛБпBCЁЂCDгкEЁЂFЃЎ
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
ЃЈ1ЃЉШчЭММзЃЌЕБЖЅЕуGдЫЖЏЕНгыЕуAжиКЯЪБЃЌЧѓжЄЃКEC+CF=BCЃЛ
ЃЈ2ЃЉжЊЪЖЬНОПЃК
ЂйШчЭМввЃЌЕБЖЅЕуGдЫЖЏЕНACЕФжаЕуЪБЃЌЧыжБНгаДГіЯпЖЮECЁЂCFгыBCЕФЪ§СПЙиЯЕЃЈВЛашвЊаДГіжЄУїЙ§ГЬЃЉЃЛ
ЂкШчЭМБћЃЌдкЖЅЕуGдЫЖЏЕФЙ§ГЬжаЃЌШє![]() ЃЌЬНОПЯпЖЮECЁЂCFгыBCЕФЪ§СПЙиЯЕЃЛ
ЃЌЬНОПЯпЖЮECЁЂCFгыBCЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉЮЪЬтНтОіЃКШчЭМБћЃЌвбжЊСтаЮЕФБпГЄЮЊ8ЃЌBG=7ЃЌCF=![]() ЃЌЕБ
ЃЌЕБ![]() ЃО2ЪБЃЌЧѓECЕФГЄЖШЁЃ
ЃО2ЪБЃЌЧѓECЕФГЄЖШЁЃ
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШ§НЧаЮABCЃЈМЧзїЁїABCЃЉдк8ЁС8ЗНИёжаЃЌЮЛжУШчЭМЫљЪОЃЌAЃЈЃ3ЃЌ1ЃЉЃЌBЃЈЃ2ЃЌ4ЃЉЃЎ

ЃЈ1ЃЉЧыФудкЗНИёжаНЈСЂжБНЧзјБъЯЕЃЌВЂаДГіCЕуЕФзјБъЃЛ
ЃЈ2ЃЉАбЁїABCЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌдйЯђгвЦНвЦ2ИіЕЅЮЛГЄЖШЃЌЧыФуЛГіЦНвЦКѓЕФЁїA1B1C1ЃЌШєЁїABCФкВПвЛЕуPЕФзјБъЮЊЃЈaЃЌbЃЉЃЌдђЕуPЕФЖдгІЕуP1ЕФзјБъЪЧ ЃЎ
ЃЈ3ЃЉдкxжсЩЯДцдквЛЕуDЃЌЪЙЁїDB1C1ЕФУцЛ§ЕШгк3ЃЌЧѓТњзуЬѕМўЕФЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com