
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÖ±Ļßy£½x+3ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬Å×ĪļĻßy£½©x2+bx+c¾¹żA”¢BĮ½µć£¬ÓėxÖį½»ÓŚĮķŅ»øöµćC£¬¶Ō³ĘÖįÓėÖ±ĻßAB½»ÓŚµćE£¬Å×ĪļĻ߶„µćĪŖD£®
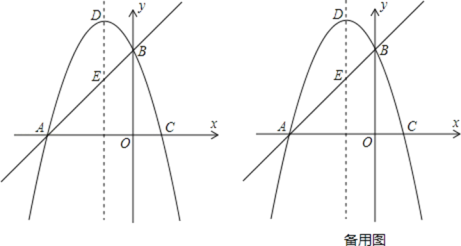
£Ø1£©µćAµÄ×ų±źĪŖ”” ””£¬µćBµÄ×ų±źĪŖ”” ””£®
£Ø2£©¢ŁĒóÅ×ĪļĻߵĽāĪöŹ½£»
¢ŚÖ±ĻßABÓėÅ×ĪļĻߵĶŌ³ĘÖį½»ÓŚµćE£¬ŌŚxÖįÉĻŹĒ·ń“ęŌŚµćM£¬Ź¹µĆME+MB×īŠ”£¬Ēó³öµćMµÄ×ų±ź£®
£Ø3£©µćP“ÓµćD³ö·¢£¬ŃŲ¶Ō³ĘÖįĻņĻĀŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶ČŌČĖŁŌĖ¶Æ£¬ÉčŌĖ¶ÆµÄŹ±¼äĪŖtĆė£¬µ±tĪŖŗĪÖµŹ±£¬ŅŌP”¢B”¢CĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£æÖ±½ÓŠ“³öĖłÓŠ·ūŗĻĢõ¼žµÄtÖµ£®
”¾“š°ø”æ£Ø1£©£Ø©3£¬0£©£¬£Ø0£¬3£©£»£Ø2£©¢Ły£½©x2©2x+3£»¢ŚM£Ø©![]() £¬0£©£»£Ø3£©µ±tĪŖ3”¢4”Ą
£¬0£©£»£Ø3£©µ±tĪŖ3”¢4”Ą![]() ”¢4ĆėŹ±£¬ŅŌP”¢B”¢CĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ
”¢4ĆėŹ±£¬ŅŌP”¢B”¢CĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ
”¾½āĪö”æ
£Ø1£©Įīx£½0£¬Ōņy£½3£¬Įīy£½0£¬Ōņx£½©3£¬¼“æÉĒó½ā£»
£Ø2£©¢ŁBµÄ×ų±źĪŖ£ŗ£Ø0£¬3£©£¬¹Źc£½3£¬½«µćAµÄ×ų±ź“śČėÅ×ĪļĻß±ķ“ļŹ½²¢½āµĆ£ŗb£½©2£¬¼“æÉĒó½ā£»
¢ŚŗÆŹżµÄ¶Ō³ĘÖįĪŖ£ŗx£½©1£¬µćE£Ø©1£¬2£©£¬µćB£Ø0£¬3£©£¬×÷µćB¹ŲÓŚxÖįµÄ¶Ō³ĘµćB”ä£Ø0£¬©3£©£¬Į¬½ÓEB”ä½»xÖįÓŚµćM£¬ŌņµćMĪŖĖłĒ󣬼“æÉĒó½ā£»
£Ø3£©·ÖPC£½PB”¢BC£½PC”¢BC£½PB£¬ČżÖÖĒéæö£¬·Ö±šĒó½ā¼“æÉ£®
½ā£ŗ£Ø1£©y£½x+3£¬Įīx£½0£¬Ōņy£½3£¬Įīy£½0£¬Ōņx£½©3£¬
¹ŹµćA”¢BµÄ×ų±ź·Ö±šĪŖ£ŗ£Ø©3£¬0£©”¢£Ø0£¬3£©£¬
¹Ź“š°øĪŖ£ŗ£Ø©3£¬0£©£¬£Ø0£¬3£©£»
£Ø2£©¢ŁBµÄ×ų±źĪŖ£ŗ£Ø0£¬3£©£¬¹Źc£½3£¬
½«µćAµÄ×ų±ź“śČėÅ×ĪļĻß±ķ“ļŹ½y£½©x2+bx+3ÖŠµĆ£ŗ-(-3)2-3b+3=0
½āµĆ£ŗb£½©2£¬
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy£½©x2©2x+3£»
¢ŚŗÆŹżµÄ¶Ō³ĘÖįĪŖ£ŗx£½©1
½«x=-1“śČė½āĪöŹ½y£½x+3µĆy=-1+3=2
”ąµćE£Ø©1£¬2£©£¬µćB£Ø0£¬3£©£¬
×÷µćB¹ŲÓŚxÖįµÄ¶Ō³ĘµćB”ä£Ø0£¬©3£©£¬Į¬½ÓEB”ä½»xÖįÓŚµćM£¬ŌņµćMĪŖĖłĒó£¬
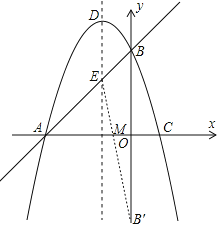
ÉčÖ±ĻßB”äEµÄ±ķ“ļŹ½ĪŖy=mx+n
½«B”ä£Ø0£¬©3£©ŗĶE£Ø©1£¬2£©“śČėµĆ£ŗ
![]()
½āµĆ![]()
ŌņÖ±ĻßB”äEµÄ±ķ“ļŹ½ĪŖ£ŗy£½©5x©3£¬
µ±y£½0Ź±£¬x£½©![]() £¬¹ŹµćM£Ø©
£¬¹ŹµćM£Ø©![]() £¬0£©£»
£¬0£©£»
£Ø3£©Įīy£½©x2©2x+3ÖŠy£½0£¬Ōņ©x2©2x+3£½©£Øx©1£©£Øx+3£©£½0£¬
½āµĆ£ŗx£½1»ņx£½©3£¬
”ąC£Ø1£¬0£©£®
”ßy£½©x2©2x+3£½©£Øx+1£©2+4£¬
”ąD£Ø©1£¬4£©£¬P£Ø©1£¬4©t£©£®
”ßB£Ø0£¬3£©£¬C£Ø1£¬0£©£¬
”ąPC2£½£Ø©1©1£©2+£Ø4©t£©2£½t2©8t+20£¬PB2£½£Ø©1£©2+£Ø4©t©3£©2£½t2©2t+2£¬BC2£½12+32£½10£®
¢Łµ±PC£½PBŹ±£¬
¼“t2©8t+20£½t2©2t+2½āµĆ£ŗt£½3£»
¢Śµ±BC£½PCŹ±£¬
¼“100= t2©8t+20½āµĆ£ŗt£½4”Ą![]() £»
£»
¢Ūµ±BC£½PBŹ±£¬
¼“100= t2©2t+2½āµĆ£ŗt£½4»ņ©2£ØÉįČ„øŗÖµ£©
×ŪÉĻæÉÖŖ£ŗµ±tĪŖ3”¢4”Ą![]() ”¢4ĆėŹ±£¬ŅŌP”¢B”¢CĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£®
”¢4ĆėŹ±£¬ŅŌP”¢B”¢CĪŖ¶„µćµÄČż½ĒŠĪŹĒµČŃüČż½ĒŠĪ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬µć
£¬µć![]() £¬
£¬![]() ·Ö±šŌŚ±ß
·Ö±šŌŚ±ß![]() £¬
£¬![]() ÉĻ£¬Ö±Ļß
ÉĻ£¬Ö±Ļß![]() ½»¾ŲŠĪ¶Ō½ĒĻß
½»¾ŲŠĪ¶Ō½ĒĻß![]() ÓŚµć
ÓŚµć![]() £¬½«
£¬½«![]() ŃŲÖ±Ļß
ŃŲÖ±Ļß![]() ·ÕŪ£¬µć
·ÕŪ£¬µć![]() ĀäŌŚµć
ĀäŌŚµć![]() “¦£¬ĒŅµć
“¦£¬ĒŅµć![]() ŌŚÉäĻß
ŌŚÉäĻß![]() ÉĻ.
ÉĻ.
£Ø1£©ČēĶ¼1ĖłŹ¾£¬µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø2£©ČēĶ¼2ĖłŹ¾£¬µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø3£©ĒėŠ“³öĻ߶Ī![]() µÄ³¤µÄȔֵ·¶Ī§£¬¼°µ±
µÄ³¤µÄȔֵ·¶Ī§£¬¼°µ±![]() µÄ³¤×ī“óŹ±
µÄ³¤×ī“óŹ±![]() µÄ³¤.
µÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÅä²Ķ¹«Ė¾ÓŠA£¬BĮ½ÖÖÓŖŃųæģ²Ķ”£Ņ»Ģģ£¬¹«Ė¾ŹŪ³öĮ½ÖÖæģ²Ķ¹²640·Ż£¬»ńĄū2160ŌŖ”£Į½ÖÖæģ²ĶµÄ³É±¾¼Ū”¢ĻśŹŪ¼ŪČēĻĀ±ķ”£
AÖÖæģ²Ķ | BÖÖæģ²Ķ | |
³É±¾¼Ū | 5ŌŖ/·Ż | 6ŌŖ/·Ż |
ĻśŹŪ¼Ū | 8ŌŖ/·Ż | 10ŌŖ/·Ż |
£Ø1£©ĒóøĆ¹«Ė¾ÕāŅ»ĢģĻśŹŪA”¢BĮ½ÖÖæģ²Ķø÷¶ąÉŁ·Ż£æ
£Ø2£©ĪŖĄ©“óĻśŹŪ£¬¹«Ė¾¾ö¶ØµŚ¶žĢģ¶ŌŅ»¶ØŹżĮæµÄA”¢BĮ½ÖÖæģ²ĶĶ¬Ź±¾ŁŠŠ½µ¼Ū“ŁĻś»ī¶Æ”£½µ¼ŪµÄA”¢BĮ½ÖÖæģ²ĶµÄŹżĮæ¾łĪŖµŚŅ»ĢģĻśŹŪA”¢BĮ½ÖÖæģ²ĶŹżĮæµÄ2±¶£¬ĒŅAÖÖæģ²Ķ°“ŌĻśŹŪ¼ŪµÄ¾ÅĪåÕŪ³öŹŪ£¬Čō¹«Ė¾ŅŖĒóÕāŠ©æģ²Ķµ±ĢģČ«²æŹŪ³öŗó£¬Ėł»ńµÄĄūČó²»ÉŁÓŚ3280ŌŖ£¬ÄĒĆ“BÖÖæģ²Ķ×īµĶæÉŅŌ°“ŌĻśŹŪ¼Ū“ņ¼øÕŪ³öŹŪ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
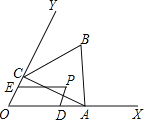
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ”ĻXOY=60”ć£¬µćAŌŚ±ßOXÉĻ£¬OA=2£®¹żµćA×÷AC”ĶOYÓŚµćC£¬ŅŌACĪŖŅ»±ßŌŚ”ĻXOYÄŚ×÷µČ±ßČż½ĒŠĪABC£¬µćPŹĒ”÷ABCĪ§³ÉµÄĒųÓņ£Ø°üĄØø÷±ß£©ÄŚµÄŅ»µć£¬¹żµćP×÷PD”ĪOY½»OXÓŚµćD£¬×÷PE”ĪOX½»OYÓŚµćE£®ÉčOD=a£¬OE=b£¬Ōņa+2bµÄȔֵ·¶Ī§ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
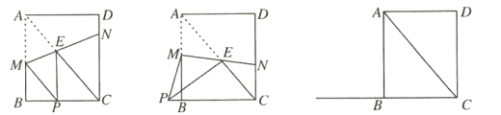
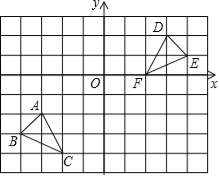
”¾ĢāÄæ”æČēĶ¼£¬·½øńÖ½ÖŠµÄĆæøöŠ”·½øń¶¼ŹĒ±ß³¤ĪŖ1øöµ„Ī»³¤¶ČµÄÕż·½ŠĪ£¬ĆæøöŠ”Õż·½ŠĪµÄ¶„µć½Šøńµć£¬”÷ABCŗĶ”÷DEFµÄ¶„µć¶¼ŌŚøńµćÉĻ£¬½įŗĻĖłøųµÄĘ½ĆęÖ±½Ē×ų±źĻµ½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©»³ö”÷ABCĻņÉĻĘ½ŅĘ4øöµ„Ī»³¤¶ČŗóĖłµĆµ½µÄ”÷A1B1C1£»
£Ø2£©»³ö”÷DEFČʵćO°“Ė³Ź±Õė·½ĻņŠż×Ŗ90”ćŗóĖłµĆµ½µÄ”÷D1E1F1£»
£Ø3£©”÷A1B1C1ŗĶ”÷D1E1F1×é³ÉµÄĶ¼ŠĪŹĒÖį¶Ō³ĘĶ¼ŠĪĀš£æČē¹ūŹĒ£¬ĒėÖ±½ÓŠ“³ö¶Ō³ĘÖįĖłŌŚÖ±ĻߵĽāĪöŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£3ÄŠ2Å®¹²5Ćūѧɜ²Ī¼Ó»ĘŹÆŹŠ½ĢÓż¾Ö¾Ł°ģµÄ”°ĪŅ°®»ĘŹÆ”±ŃŻ½²±ČČü£®
£Ø1£©Čō“Ó5Ćūѧɜ֊ČĪŅā³éČ”3Ćū£¬¹²ÓŠ¶ąÉŁÖÖ²»Ķ¬µÄ³é·Ø£¬ĮŠ³öĖłÓŠæÉÄÜĒéŠĪ£»
£Ø2£©Čō³éČ”µÄ3Ćūѧɜ֊£¬Ä³ÄŠÉś³éÖŠ£¬ĒŅ±ŲÓŠ1Å®ÉśµÄøÅĀŹŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
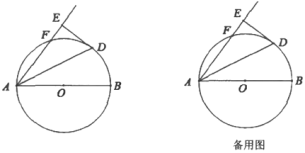
”¾ĢāÄæ”æČēĶ¼Ź¾£¬![]() ŹĒ
ŹĒ![]() µÄÖ±¾¶£¬µć
µÄÖ±¾¶£¬µć![]() ŹĒ°ėŌ²ÉĻµÄŅ»¶Æµć£Ø
ŹĒ°ėŌ²ÉĻµÄŅ»¶Æµć£Ø![]() ²»Óė
²»Óė![]() £¬
£¬![]() ÖŲŗĻ£©£¬ĻŅ
ÖŲŗĻ£©£¬ĻŅ![]() Ę½·Ö
Ę½·Ö![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ½»ÉäĻß
½»ÉäĻß![]() ÓŚµć
ÓŚµć![]() .
.
£Ø1£©ĒóÖ¤£ŗ![]() Óė
Óė![]() ĻąĒŠ£ŗ
ĻąĒŠ£ŗ
£Ø2£©Čō![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() ³¤£»
³¤£»
£Ø3£©Čō![]() £¬
£¬![]() ³¤¼ĒĪŖ
³¤¼ĒĪŖ![]() £¬
£¬![]() ³¤¼ĒĪŖ
³¤¼ĒĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³ö![]() µÄ×ī“óÖµ.
µÄ×ī“óÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
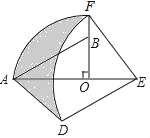
”¾ĢāÄæ”æČēĶ¼£¬ŌŚRt”÷AOBÖŠ£¬”ĻAOB=90”ć£¬OA=3£¬OB=2£¬½«Rt”÷AOBČʵćOĖ³Ź±ÕėŠż×Ŗ90”ćŗóµĆRt”÷FOE£¬½«Ļ߶ĪEFČʵćEÄꏱÕėŠż×Ŗ90”ćŗóµĆĻ߶ĪED£¬·Ö±šŅŌO£¬EĪŖŌ²ŠÄ£¬OA”¢ED³¤ĪŖ°ė¾¶»»”AFŗĶ»”DF£¬Į¬½ÓAD£¬ŌņĶ¼ÖŠŅõÓ°²æ·ÖĆ껿ŹĒ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
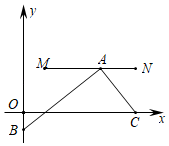
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬M”¢N”¢CČżµćµÄ×ų±ź·Ö±šĪŖ£Ø![]() £¬1£©£¬£Ø3£¬1£©£¬£Ø3£¬0£©£¬µćAĪŖĻ߶ĪMNÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓAC£¬¹żµćA×÷AB”ĶAC½»yÖįÓŚµćB£¬µ±µćA“ÓMŌĖ¶Æµ½NŹ±£¬µćBĖęÖ®ŌĖ¶Æ£¬ÉčµćBµÄ×ų±źĪŖ£Ø0£¬b£©£¬ŌņbµÄȔֵ·¶Ī§ŹĒ£Ø””””£©
£¬1£©£¬£Ø3£¬1£©£¬£Ø3£¬0£©£¬µćAĪŖĻ߶ĪMNÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓAC£¬¹żµćA×÷AB”ĶAC½»yÖįÓŚµćB£¬µ±µćA“ÓMŌĖ¶Æµ½NŹ±£¬µćBĖęÖ®ŌĖ¶Æ£¬ÉčµćBµÄ×ų±źĪŖ£Ø0£¬b£©£¬ŌņbµÄȔֵ·¶Ī§ŹĒ£Ø””””£©
A.![]() ӆbӆ1B.
ӆbӆ1B.![]() ӆbӆ1C.
ӆbӆ1C.![]() ӆbӆ
ӆbӆ![]() D.
D.![]() ӆbӆ1
ӆbӆ1
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com