
分析 先点A(m,p),B(n,q)(m<n<0)在动点C($\frac{k}{a}$,a)(k≠0)所形成的曲线上得出m与p、n与q的表达式,再根据p+q=-b-2,$\frac{m+n}{mn}=\frac{{{b^2}+b}}{k}$-1可得出关于k的表达式,进而判断出k的符号,根据反比例函数的性质即可得出结论;
解答 解:∵A(m,p),B(n,q)(m<n<0)在动点C($\frac{k}{a}$,a)(k≠0)所形成的曲线上.
∴p=$\frac{k}{m}$,q=$\frac{k}{n}$.
∴p+q=$\frac{k(m+n)}{mn}$.
∵p+q=-b-2,
∴-b-2=k•($\frac{{b}^{2}+b}{k}$-1),
∴k=b2+2b+2=(b+1)2+1>0,
∵m<n<0,p=$\frac{k}{m}$,q=$\frac{k}{n}$.
∴p>q.
点评 本题考查的是反比例函数综合题,熟知反比例函数的增减性、反比例函数图象上点的坐标特点等知识是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x-y=y+3\\ x-y=45+x\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-y=y+3\\ x-y=45-x\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y=y-3\\ x-y=45+x\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=y-3\\ x-y=45-x\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
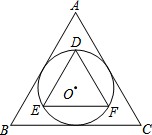 如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.
如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
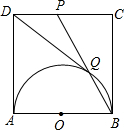 如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号)
如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com