
���� �������������ĵ����ʶԢٽ����жϣ��������������ߵĹ�ϵ���ʹ�ʽ�Ԣڽ����жϣ��������ߵ����ʺ������������ʽ�Ԣ۽����жϣ��������ƵĶ����ȫ�ȵ��ж������Ԣܽ����жϣ�������ѧ�����������ε��ж�������������ȫ�ȵķ����Ԣݽ����жϣ�������Գ�ͼ�κ��ĶԳ�ͼ�εĶ���Ԣ����жϣ�
��� �⣺�������������������ߵĽ��㣬���������ε�ÿ�����߳���Ϊ1��2�����Ԣ�Ϊ�����⣻
���ĸ�����2��3��4��5��ľ��������4�ֵȿ��ܵĽ������������Χ�������εĸ�����$\frac{3}{4}$�����Ԣ�Ϊ�����⣻
ֱ�������ε�����Բ�뾶Ϊ����ֱ�DZߵĻ����ܳ����̣����Ԣ�Ϊ�����⣻
���������β�һ����ȫ�������Σ�ȫ��������һ�������������Σ����Ԣ�Ϊ�����⣻
������ѧ�ж��������������Ƶķ�����3�֣��ж�����������ȫ�ȵķ�����5�֣����Ԣ�Ϊ�����⣻
�ȱ�����������Գ�ͼ�Σ��������ĶԳ�ͼ�Σ����Ԣ�Ϊ�����⣮
�ʴ�Ϊ�ۢܢݢޣ�
���� ���⿼���������붨�����ж�һ���������䣬�������⣮�������ⶼ��������ͽ�����������ɣ���������֪�������������֪�����Ƴ������һ���������д�ɡ��������ô������ʽ����Щ�������ȷ����������֤ʵ�ģ����������������������


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��$\frac{1}{2}$ | B�� | m��$\frac{1}{2}$ | C�� | m��-$\frac{1}{2}$ | D�� | m��-$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
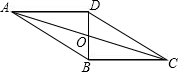 ��ͼ���ı���ABCD��ƽ���ı��Σ��Խ���AC��BD�ཻ�ڵ�O��BD��AD��AD=6��AB=10����DC��BC��ƽ���ı���ABCD�������
��ͼ���ı���ABCD��ƽ���ı��Σ��Խ���AC��BD�ཻ�ڵ�O��BD��AD��AD=6��AB=10����DC��BC��ƽ���ı���ABCD��������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com