
分析 由a2+11a=-16,b2+11b=-16可知a、b为方程x2+11x+16的两个根,由根与系数的关系可得出a+b=-11,ab=16,再将$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$化简成$\sqrt{\frac{(a+b)^{2}}{ab}}$,代入a+b=-11、ab=16即可得出结论.
解答 解:∵a2+11a=-16,b2+11b=-16,
∴a、b为方程x2+11x+16的两个根,
∴a+b=-11,ab=16.
$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\sqrt{(\sqrt{\frac{b}{a}}+\sqrt{\frac{a}{b}})^{2}}$=$\sqrt{\frac{b}{a}+\frac{a}{b}+2}$=$\sqrt{\frac{{a}^{2}+{b}^{2}+2ab}{ab}}$=$\sqrt{\frac{(a+b)^{2}}{ab}}$,
将a+b=-11,ab=16代入$\sqrt{\frac{(a+b)^{2}}{ab}}$中得:
$\sqrt{\frac{b}{a}}$+$\sqrt{\frac{a}{b}}$=$\frac{11}{4}$
点评 本题考查了根与系数的关系以及二次根式的化简求值,解题的关键是找出a+b=-11,ab=16.本题属于基础题,难度不大,解决该题型题目时,由根与系数的关系找出两根之和与两根之积是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{7x>98}\\{7(x+3)>98}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7x<98}\\{7(x+3)>98}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{7x<98}\\{7x+3>98}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x>98}\\{7x+3<98}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个四边形的纸片ABCD,其中∠B=∠D=90°,把纸片按如图所示折叠,点B落在AD边上的E点,AF是折痕.
一个四边形的纸片ABCD,其中∠B=∠D=90°,把纸片按如图所示折叠,点B落在AD边上的E点,AF是折痕.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
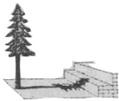 在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )| A. | 6.93米 | B. | 8米 | C. | 11.8米 | D. | 12米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com