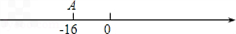A-B-E-D-C-A和A-C-D-E-B-A
分析:首先利用列举法表示出所有的路线,然后求得每条路线的费用,即可确定路费最省的路线.
解答:
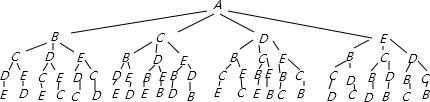
解:路线A-B-C-D-E-A的费用是:30+15+15+15+60=135元;
路线A-B-C-E-D-A的费用是:30+15+25+15+50=135元;
路线A-B-D-C-E-A的费用是:30+25+15+25+60=155元;
路线A-B-D-E-C-A的费用是:30+25+15+25+40=135元;
路线A-B-E-D-C-A的费用是:30+30+15+15+40=130元;
路线A-B-E-C-D-A的费用是:30+30+25+15+50=150元;
路线A-C-B-D-E-A的费用是:40+15+25+15+60=155元;
路线A-C-B-E-D-A的费用是:40+15+30+15+50=150元;
路线A-C-D-B-E-A的费用是:40+15+25+30+60=170元;
路线A-C-D-E-B-A的费用是:40+15+15+30+30=130元;
路线A-C-E-B-D-A的费用是:40+25+30+25+50=170元;
路线A-C-E-D-B-A的费用是:40+25+15+25+30=135元;
路线A-D-B-C-E-A的费用是:50+25+15+25+60=175元;
路线A-D-B-E-C-A的费用是:50+25+30+25+40=170元;
路线A-D-C-B-E-A的费用是:50+15+15+30+60=170元;
路线A-D-C-E-B-A的费用是:50+15+25+30+30=150元;
路线A-D-E-B-C-A的费用是:50+15+30+15+40=150元;
路线A-D-E-C-B-A的费用是:50+15+25+15+30=135元;
路线A-E-B-C-D-A的费用是:60+30+15+15+50=170元;
路线A-E-B-D-C-A的费用是:60+30+25+15+40=170元;
路线A-E-C-B-D-A的费用是:60+25+15+25+50=175元;
路线A-E-C-D-B-A的费用是:60+25+15+25+30=155元;
路线A-E-D-B-C-A的费用是:60+15+25+15+40=155元;
路线A-E-D-C-B-A的费用是:60+15+15+15+30=135元;
故费用最少的路线是:A-B-E-D-C-A和A-C-D-E-B-A.
故答案是:A-B-E-D-C-A和A-C-D-E-B-A.
点评:本题主要考查了列举法以及有理数的加法计算,关键是利用列举法列举出所有的路线.

 解:路线A-B-C-D-E-A的费用是:30+15+15+15+60=135元;
解:路线A-B-C-D-E-A的费用是:30+15+15+15+60=135元;

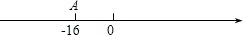 退4米…,按此规律行进,如果A地在数轴上表示的数为-16,
退4米…,按此规律行进,如果A地在数轴上表示的数为-16, 退4米…,按此规律行进,如果A地在数轴上表示的数为-16,
退4米…,按此规律行进,如果A地在数轴上表示的数为-16,