
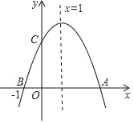
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a﹣2b+c<0;③b2﹣4ac>0;④当y<0时,x<﹣1或x>2.其中正确的有( )
A. 4个B. 3个C. 2个D. 1个
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】有一条抛物线,三位学生分别说出了它的一些性质:甲说:对称轴是直线![]() ;乙说:与
;乙说:与![]() 轴的两个交点的距离为6;丙说:顶点与
轴的两个交点的距离为6;丙说:顶点与![]() 轴的交点围成的三角形面积等于9,则这条抛物线解析式的顶点式是______.
轴的交点围成的三角形面积等于9,则这条抛物线解析式的顶点式是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
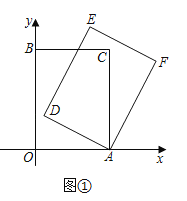
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)在解一元二次方程的时候,发现有一类形如x2+(m+n)x+mn=0的方程,其常数项是两个因数的积,而它的一次项系数恰好是这两个因数的和,则我们可以把它转化成x2+(m+n)x+mn=(m+x)(m+n)=0
(探索)解方程:x2+5x+6=0:x2+5x+6=x2+(2+3)x+2×3=(x+2)(x+3),原方程可转化为(x+2)(x+3)=0,即x+2=0或x+3=0,进而可求解.
(归纳)若x2+px+q=(x+m)(x+n),则p= q= ;
(应用)
(1)运用上述方法解方程x2+6x+8=0;
(2)结合上述材料,并根据“两数相乘,同号得正,异号得负“,求出一元二次不等式x2﹣2x﹣3>0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
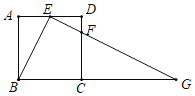
【题目】如图,在正方形ABCD中,E为边AD上的点,点F在边CD上,且CF=3FD,∠BEF=90°
(1)求证:△ABE∽△DEF;
(2)若AB=4,延长EF交BC的延长线于点G,求BG的长
查看答案和解析>>
科目:初中数学 来源: 题型:
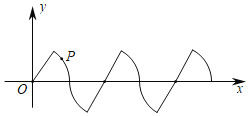
【题目】如图所示,在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒2个单位长度,点在弧线上的速度为每秒![]() 个单位长度,则第2018秒时,点P的坐标是_____.
个单位长度,则第2018秒时,点P的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足a+b+c=0,我们称这个方程为“凤凰”方程.已知
满足a+b+c=0,我们称这个方程为“凤凰”方程.已知![]() 是凤凰方程,且有两个相等的实数根,则下列正确的是( )
是凤凰方程,且有两个相等的实数根,则下列正确的是( )
A.a=cB.a=bC.b=cD.a=b=c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则下列代数式:ab,ac,a+b+c,a-b+c, 2a+b,2a-b中,其值为正的代数式的个数为( )
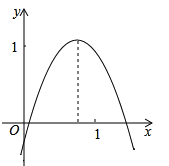
A.2个B.3个C.4个D.4个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠ACB=90°,点D为AB边上的动点(点D不与点A,点B重合),过点D作ED⊥CD交直线AC于点E,已知∠A=30°,AB=4cm,在点D由点A到点B运动的过程中,设AD=xcm,AE=ycm.
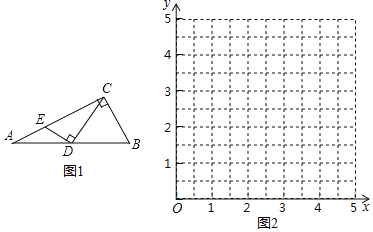
(1)通过取点、画图、测量,得到了x与y的几组值,如表:

小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:(说明:补全表格时相关数值,保留一位小数)
(2)在如图2的平面直角坐标系xOy中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为 cm.
AD时,AD的长度约为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com