Question

2．已知：如图，在Rt△ABC中，∠C=90°，BC=6，AC=8，P是斜边AB上的中点，以P为顶点，作∠MPN=∠A．∠MPN的两边分别交AC于点M、N．
（1）当△MPN是直角三角形时，求CM的长；
（2）当∠MPN绕点P转动时，设CN=x，AM=y，写出y关于x的函数解析式，并写出它的定义域；
（3）连结BM，是否存在点M，使△BMP与△ANP相似？若存在，请求出x的值；若不存在，请说明理由．

Answer 1

分析 （1）分∠PMN=90°和∠PNM=90°两种情况，根据直角三角形的性质和相似三角形的性质解答；
（2）连接CP，证明△CPN∽△AMP，根据相似三角形的对应边成比例计算即可；
（3）分△BMP∽△ANP和△BMP∽△APN两种情况讨论，根据相似三角形的判定和性质解答．

解答 解：（1）当∠PMN=90°时，
∵∠C=90°，
∴PM∥BC，P是斜边AB上的中点，
∴CM=$\frac{1}{2}$AC=4，
当∠PNM=90°时，
∴PN=$\frac{1}{2}$BC=3，
∵∠PNM=∠C，∠MPN=∠A，
∴△PNM∽△ACB，
∴$\frac{PN}{AC}$=$\frac{MN}{BC}$，
∴MN=$\frac{9}{4}$，
则CM=4-$\frac{9}{4}$=$\frac{7}{4}$，
∴CM的长为$\frac{7}{4}$或4；
（2）连接CP，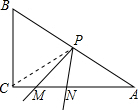
∵∠C=90°，BC=6，AC=8，
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=10，
∵P是斜边AB上的中点，
∴AP=PB=CP=5，
∵∠PCA=∠PAC，
又∵∠MPN=∠A，
∴∠CPN=∠AMP，
又∵∠PCA=∠PAC，
∴△CPN∽△AMP，
∴$\frac{CP}{AM}$=$\frac{CN}{AP}$，即$\frac{5}{y}$=$\frac{x}{5}$，
∴$\frac{25}{x}$（$\frac{25}{8}$≤x≤8）；
（3）①当△BMP∽△ANP，
则∠MBP=∠A，
∴MB=MA，
则BM²=（8-AM）²+BC²，
解得AM=$\frac{25}{4}$，即y=$\frac{25}{4}$，
∴x=4；
②，当△BMP∽△APN，
则∠BMP=∠A，
∴△BMP∽△BAM，
$\frac{BM}{AB}$=$\frac{BP}{BM}$，
∴BM=5$\sqrt{2}$，CM=$\sqrt{B{M}^{2}-B{C}^{2}}$=$\sqrt{14}$，
则AM=8-$\sqrt{14}$=y，
则$x=\frac{{8+\sqrt{14}}}{2}$．
答：$x=\frac{{8+\sqrt{14}}}{2}$或4时，△BMP与△ANP相似．

点评 本题考查的是相似三角形知识的综合运用，掌握相似三角形的判定定理和性质定理、正确运用分情况讨论思想是解题的关键．