
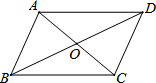
 如图,下列四组条件中,能判定?ABCD是正方形的有( )
如图,下列四组条件中,能判定?ABCD是正方形的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据平行四边形的性质,矩形、菱形以及正方形的判定方法对各组条件进行判断即可得出答案.
解答 解:①AB=BC,∠A=90°;
根据有一个角是直角且有一组邻边相等的平行四边形是正方形,能判定?ABCD是正方形,故此选项正确;
②AC⊥BD,AC=BD;
由对角线互相垂直的平行四边形是菱形,对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定?ABCD是正方形,故此选项正确;
③OA=OD,BC=CD;
由ABCD是平行四边形,可得AC与BD互相平分,而OA=OD,所以AC=BD,对角线相等的平行四边形是矩形,有一组邻边相等的平行四边形是菱形,既是矩形又是菱形的四边形是正方形,能判定?ABCD是正方形,故此选项正确;
④∠BOC=90°,∠ABD=∠DCA;
由∠BOC=90°,根据对角线互相垂直的平行四边形是菱形,可得?ABCD是菱形;由ABCD是平行四边形,可得AC与BD互相平分,AB∥CD,则∠ABD=∠CDB=∠DCA,所以OC=OD,又对角线相等的平行四边形是矩形,既是菱形又是矩形的四边形是正方形,能判定?ABCD是正方形,故此选项正确.
故选D.
点评 本题主要考查了正方形的判别方法,正方形的判定方法有:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个菱形有一个角为直角;
③还可以先判定四边形是平行四边形,再用1或2进行判定.


科目:初中数学 来源: 题型:选择题
| A. | a=10 | B. | a=4 | C. | a≥9 | D. | a≥10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点,点O是在△ABC的内部的一个动点,连接OA、OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{-3}=-\root{3}{-3}$ | B. | $\root{3}{-3}=\root{3}{3}$ | C. | $\root{3}{-3}=\root{3}{{|{-3}|}}$ | D. | $\root{3}{-3}=-\root{3}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:
某化妆品公司每月付给销售人员的工资有两种方案.方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成.设x(件)是销售商品的数量,y(元)是销售人员的月工资.如图所示,y1为方案一的函数图象,y2为方案二的函数图象.已知每件商品的销售提成方案二比方案一少7元.从图中信息解答如下问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
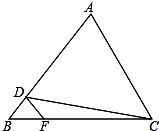 如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )
如图,在△ABC中,D、F分别是AB、BC上的点,且DF∥AC,若S△BDF:S△DFC=1:4,则S△BDF:S△DCA=( )| A. | 1:16 | B. | 1:18 | C. | 1:20 | D. | 1:24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com