
 ��ͼ��ƽ��ֱ������ϵ�У�ֱ��y=-$\sqrt{3}x$+$\sqrt{3}$��������ֱ��ڵ�A��B���ҵ�C��x�Ḻ�����ϣ���AB��AC=1��2��
��ͼ��ƽ��ֱ������ϵ�У�ֱ��y=-$\sqrt{3}x$+$\sqrt{3}$��������ֱ��ڵ�A��B���ҵ�C��x�Ḻ�����ϣ���AB��AC=1��2������ ��1����ֱ�߽���ʽ���������A�����꣬�ɹ��ɶ������AB�������AC���ó�OC�����ɵó���C�����ꣻ
��2���������ABC=90�㣬������������ǣ���M���߶�BC�ϣ���M���߶�BC�ӳ����ϣ���ʾ��BM�����������������ʽ�ֱ��ʾ��S��t�ĺ�����ϵʽ���ɣ�
��3����P��y���ϵĵ㣬������ƽ���ڴ��ڵ�Q��ʹ��A��B��P��QΪ������ı��������Σ�������������������ε��������AQ�ij�������AQ��y��ƽ�еõ�Q��A��������ͬ�������������Q�����꼴�ɣ�
��� �⣺��1������ֱ��y=-$\sqrt{3}x$+$\sqrt{3}$����y=0ʱ��-$\sqrt{3}x$+$\sqrt{3}$=0��
��ã�x=1��
��A��������1��0����
��OA=1��
��x=0ʱ��y=$\sqrt{3}$��
��B��0��$\sqrt{3}$����
��OB=$\sqrt{3}$��
�ߡ�AOB=90�㣬
��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2��
��AB��AC=1��2��
��AC=4��
��OC=3��
���C��������-3��0����
��2����ͼ1��ʾ����OA=1��OB=$\sqrt{3}$��AB=2��
���ABO=30�㣬
ͬ����BC=2$\sqrt{3}$����OCB=30�㣬 ���OBC=60�㣬
���OBC=60�㣬
���ABC=90�㣬
������������ǣ�����M���߶�BC��ʱ��BC=2$\sqrt{3}$��CM=t����BM=BC-CM=2$\sqrt{3}$-t��
��ʱS��ABM=$\frac{1}{2}$BM•AB=$\frac{1}{2}$����2$\sqrt{3}$-t����2=2$\sqrt{3}$-t��0��t��2$\sqrt{3}$����
����M��BC�ӳ�����ʱ��BC=2$\sqrt{3}$��CM=t����BM=CM-BC=t-2$\sqrt{3}$��
��ʱS��ABM=$\frac{1}{2}$BM•AB=$\frac{1}{2}$����t-2$\sqrt{3}$����2=t-2$\sqrt{3}$��t��2$\sqrt{3}$����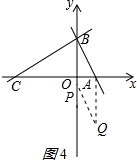 ��3��P��y���ϵĵ㣬������ƽ���ڴ��ڵ�Q��ʹ�� A��B��P��QΪ������ı��������Σ�
��3��P��y���ϵĵ㣬������ƽ���ڴ��ڵ�Q��ʹ�� A��B��P��QΪ������ı��������Σ�
��P��y���������ϣ��ı���ABPQΪ����ʱ��
����ͼ2��ʾ��AQ=AB=2����Q��A�ĺ�������ͬ��
��ʱQ����Ϊ��1��2����
����ͼ3��ʾ��AP=AQ=$\frac{2\sqrt{3}}{3}$��Q��A�ĺ�������ͬ��
��ʱQ����Ϊ��1��$\frac{2\sqrt{3}}{3}$����
��P��y�Ḻ�����ϣ��ı���ABPQΪ����ʱ��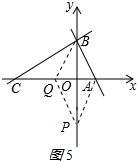 ����ͼ4��ʾ��AQ=AB=2����Q��A��������ͬ��
����ͼ4��ʾ��AQ=AB=2����Q��A��������ͬ��
��ʱQ����Ϊ��1��-2����
����ͼ5��ʾ��BP��ֱƽ��AQ��
��ʱQ����Ϊ��-1��0����
������������������Q������1��2������1��-2������1��$\frac{2\sqrt{3}}{3}$������-1��0����
���� ������һ�κ����ۺ��⣬������ֱ�������ε����ʡ����ɶ�����������ͼ�����ʡ�ֱ�������ε��ж������ε����ʵ�֪ʶ�������ۺ���ǿ���ѶȽϴ��ر��ǣ�2����3���У���Ҫ����ͼ�Σ����з������۲��ܵó������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}\sqrt{3}$ | B�� | 3$\sqrt{3}$ | C�� | 6$\sqrt{3}$ | D�� | 12$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
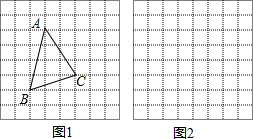
 ��ͼ����ֱ�ǡ�ABC�У���ACB=90�㣬��BAC��ƽ���߽�BC��D��CE��AB�ڵ�E����AD�ڵ�F��ȡBG=CD������FG����֤��FG��AB��
��ͼ����ֱ�ǡ�ABC�У���ACB=90�㣬��BAC��ƽ���߽�BC��D��CE��AB�ڵ�E����AD�ڵ�F��ȡBG=CD������FG����֤��FG��AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{106960}{x+500}$-$\frac{50760}{x}$=20 | B�� | $\frac{50760}{x}$-$\frac{106960}{x+500}$=20 | ||
| C�� | $\frac{106960}{x+20}$-$\frac{50760}{x}$=500 | D�� | $\frac{50760}{x}$-$\frac{106960}{x+20}$=500 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com