
分析 根据规律可知全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数.归纳可得第n组的第一个数为4n(n≥2),又因为20=3×6+2,所以第20个智慧数是第7组中的第2个数,从而得到4×7+1=29.
解答 解:∵第1个智慧数3=22-12,第2个智慧数5=32-22,第3个智慧数7=42-32,
第4个智慧数8=32-12,第5个智慧数9=52-42,第6个智慧数11=62-52,
第7个智慧数12=42-22,第8个智慧数13=72-62,第9个智慧数15=42-12,
第10个智慧数16=52-32,第11个智慧数17=92-82,第12个智慧数19=102-92,
…
∴可知全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数.
即第n组的第一个数为4n(n≥2),
∵20=3×6+2,
∴第20个智慧数位于第7组第2个数,
∵第7组的第1个智慧数为4×7=28,
∴第7组第2个数为29,即第20个智慧数为29,
故答案为:29.
点评 本题主要考查数字的变化规律,将全部智慧数从小到大可按每三个数分一组,从第2组开始每组的第一个数都是4的倍数是解题的关键.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:解答题
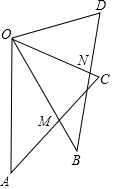 已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.
已知:如图,OA=OB,OC=OD,∠AOB=∠BOC=∠COD,线段AC交线段OB于点M,线段BD交线段OC于点N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{8}$=2$\sqrt{2}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com