
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径 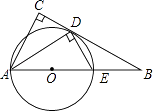
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
【答案】
(1)解:结论:BC与⊙O相切.
证明:如图连接OD.
∵OA=OD,
∴∠OAD=∠ODA,
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∵AC⊥BC,
∴OD⊥BC.
∴BC是⊙O的切线

(2)解:∵BC是⊙O切线,
∴∠ODB=90°,
∴∠BDE+∠ODE=90°,
∵AE是直径,
∴∠ADE=90°,
∴∠DAE+∠AED=90°,
∵OD=OE,
∴∠ODE=∠OED,
∴∠BDE=∠DAB,
∵∠B=∠B,
∴△ABD∽△DBE
(3)解:在Rt△ODB中,∵cosB= ![]() =
= ![]() ,设BD=2
,设BD=2 ![]() k,OB=3k,
k,OB=3k,
∵OD2+BD2=OB2,
∴4+8k2=9k2,
∴k=2,
∴BO=6,BD=4 ![]() ,
,
∵DO∥AC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴CD= ![]() .
.
【解析】(1)结论:BC与⊙O相切,连接OD只要证明OD∥AC即可.(2)欲证明△ABD∽△DBE,只要证明∠BDE=∠DAB即可.(3)在Rt△ODB中,由cosB= ![]() =
= ![]() ,设BD=2
,设BD=2 ![]() k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得
k,OB=3k,利用勾股定理列出方程求出k,再利用DO∥AC,得 ![]() =
= ![]() 列出方程即可解决问题.本题考查圆的综合题、切线的判定、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,学会用方程的思想思考问题,属于中考常考题型.
列出方程即可解决问题.本题考查圆的综合题、切线的判定、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,学会添加常用辅助线,学会用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.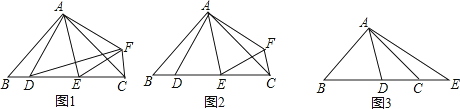
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3 ![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=40°,AD是BC边上的高,且∠DAC=20°,则∠BAC=________.
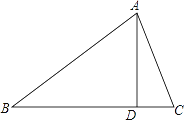
【答案】70°
【解析】∵∠B=40°,AD⊥BC,
∴∠BAD=90°-40°=50°.
∵∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°.
【题型】填空题
【结束】
16
【题目】如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
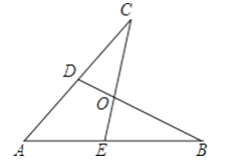
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图示的方格纸中,(1)画出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
(3)在直线MN上找一点P,使得PB+PA最短.(不必说明理由).
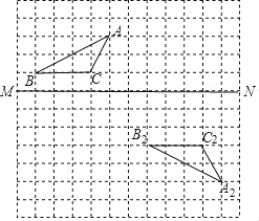
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 . 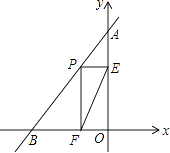
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
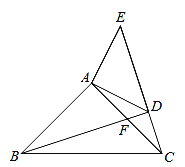
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定: ![]() (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如: ![]() ,已知T(1,﹣1)=﹣2,T(4,2)=1
,已知T(1,﹣1)=﹣2,T(4,2)=1
(1)求a,b的值;
(2)若关于m的不等式组 ![]() 恰好有4个整数解,求实数p的取值范围.
恰好有4个整数解,求实数p的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com