
分析 ①根据平方差公式求出即可;
②先找出分母有理化因式,再分子和分母都乘以有理化因式即可;
③先分母有理化,再合并即可.
解答 解:①($\sqrt{2}$+1)($\sqrt{2}$-1)=($\sqrt{2}$)2-12=1,
($\sqrt{2}$+$\sqrt{3}$)($\sqrt{3}$-$\sqrt{2}$)=($\sqrt{3}$)2-($\sqrt{2}$)2=1.
故答案为:1,1;
②$\frac{1}{\sqrt{3}+2}$=$\frac{1×(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$.
故答案为:2-$\sqrt{3}$;
③原式=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$+$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$+…+$\frac{1×(\sqrt{2012}-\sqrt{2011})}{(\sqrt{2012}+\sqrt{2011})(\sqrt{2012}-\sqrt{2011})}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2012}$-$\sqrt{2011}$
=$\sqrt{2012}$-1.
点评 本题考查了二次根式的混合运算,平方差公式,分母有理化的应用,能找出分母的有理化因式是解此题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
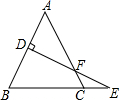 如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=50°,AB+BC=6cm,则△BCF的周长为6cm,∠EFC的度数为40°.
如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=50°,AB+BC=6cm,则△BCF的周长为6cm,∠EFC的度数为40°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
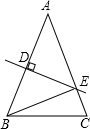 如图,在△ABC中,AC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,EC=2cm,则BE的长为( )
如图,在△ABC中,AC=8cm,AB的垂直平分线交AB于点D,交边AC于点E,EC=2cm,则BE的长为( )| A. | 4cm | B. | 5cm | C. | 6cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com