
【题目】【问题】如图①,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=80°,则∠BEC=__ __;若∠A=n°,则∠BEC=__ _.
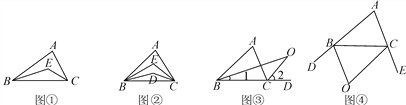
【探究】
(1)如图②,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB.若∠A=n°,则∠BEC=____;
(2)如图③,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图④,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
【答案】问题:130°,90°+![]() n°探究:(1)60°+
n°探究:(1)60°+![]() n°(2)∠BOC=
n°(2)∠BOC=![]() ∠A. (3)∠BOC=90°-
∠A. (3)∠BOC=90°-![]() ∠A
∠A
【解析】试题分析:问题:利用三角形的内角和等于180°求出∠ABC+∠ACB,再利用角平分线的定义求出∠EBC+∠ECB,然后根据三角形的内角和等于180°列式计算即可得解;将∠A的度数换成n°,然后求解即可;
探究:(1)利用三角形的内角和等于180°求出∠ABC+∠ACB,再利用三等分角求出∠EBC+∠ECB,然后根据三角形的内角和等于180°列式计算即可得解;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ACD和∠OCD,再根据角平分线的定义可得∠ABC=2∠OBC,∠ACD=2∠OCD,然后整理即可得解;
(3)根据平角的定义以及角平分线的定义表示出∠OBC和∠OCB,然后根据三角形的内角和定理列式表示出∠BOC,然后整理即可得解.
试题解析:【问题】解:∵∠A=80°,
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×100°=50°,
×100°=50°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-50°=130°;
由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A=180°-n°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(180°-n°)=90°-
×(180°-n°)=90°-![]() n°,
n°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-(90°-![]() n°)=90°+
n°)=90°+![]() n°;
n°;
探究:解:(1)由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A=180°-n°,
∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,
∴∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB,
∠ACB,
∴∠EBC+∠ECB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×(180°-n°)=120°-
×(180°-n°)=120°-![]() n°,
n°,
∴∠BEC=180°-(∠EBC+∠ECB)=180°-(120°-![]() n°)=60°+
n°)=60°+![]() n°;
n°;
(2)∠BOC=![]() ∠A.
∠A.
理由如下:由三角形的外角性质得,∠ACD=∠A+∠ABC,
∠OCD=∠BOC+∠OBC,
∵O是∠ABC与外角∠ACD的平分线BO和CO的交点,
∴∠ABC=2∠OBC,∠ACD=2∠OCD,
∴∠A+∠ABC=2(∠BOC+∠OBC),
∴∠A=2∠BOC,
∴∠BOC=![]() ∠A;
∠A;
(3)∵O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,
∴∠OBC=![]() (180°-∠ABC)=90°-
(180°-∠ABC)=90°-![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() (180°-∠ACB)=90°-
(180°-∠ACB)=90°-![]() ∠ACB,
∠ACB,
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-(90°-![]() ∠ABC)-(90°-
∠ABC)-(90°-![]() ∠ACB)=
∠ACB)=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
由三角形的内角和定理得,∠ABC+∠ACB=180°-∠A,
∴∠BOC=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
【题目】如图示我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为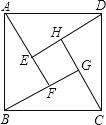
查看答案和解析>>
科目:初中数学 来源: 题型:
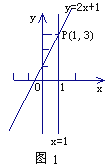
【题目】阅读,我们知道,在数轴上,x=1表示一个点,而在平面坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形,就是一次函数y=2x+1的图象,它也是一条直线,如图1,可以得出,直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组![]() 的解,所以这个方程组的解为
的解,所以这个方程组的解为![]()
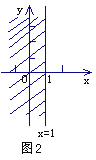
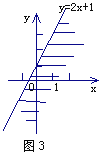
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧的部分,如图2;y≤2x+1,也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3.
回答下列问题:
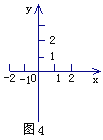
(1)在直角坐标系(如图4)中,用作图的方法求方程组![]() 的解;
的解;
(2)用阴影表示 所围成的区域.
所围成的区域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,第一个正方形的顶点A1(﹣1,1),B1(1,1);第二个正方形的顶点A2(﹣3,3),B2(3,3);第三个正方形的顶点A3(﹣6,6),B3(6,6)按顺序取点A1,B2,A3,B4,A5,B6…,则第12个点应取点B12,其坐标为( )

A. (12,12) B. (78,78) C. (66,66) D. (55,55)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L:y=-![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠A=60°,过点C作⊙O的切线,交射线BO于点E. 
(1)求∠BCE的度数;
(2)若⊙O半径为3,求BE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
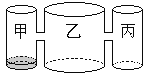
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com