
【题目】如图在矩形 ABCD 中 AB=8,BC=6,AE=BE,点 F 为边 BC 上任意一点,将BEF 沿着 EF 翻折,点 B 为点 B 的对应点,则当BCD 的面积最小时BCF 的面积为( )

A.4B.6C.4.2D.3
【答案】A
【解析】
当△B′CD面积最小时,B′到CD的距离最小,即B′到AB的距离最大,当B′到AB的距离=EB′时,此时B′到AB的距离最大,即EB′⊥AB,根据折叠的性质得到BE=B′E,∠B=∠EB′F=∠B′EB=90![]() ,推出四边形EBFB′是正方形,得到B’F=BE=4,FC=BC-BF=2,于是得到BCF 的面积.
,推出四边形EBFB′是正方形,得到B’F=BE=4,FC=BC-BF=2,于是得到BCF 的面积.
当△B′CD面积最小时,B′到CD的距离最小,即B′到AB的距离最大,
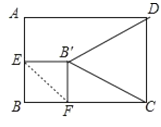
∴当B′到AB的距离=EB′时,此时B′到AB的距离最大,
即EB′⊥AB,
∵将△BEF沿EF翻折,点B的对应点为B′,
∴BE=B′E,∠B=∠EB′F=∠B′EB=90![]() ,
,
∴四边形EBFB′是正方形,
∴B’F=BE=![]() AB=4=BF,FC=BC-BF=2,
AB=4=BF,FC=BC-BF=2,
∴当△B′CD面积最小时BCF 的面积=![]() FC×B’F=
FC×B’F=![]() ×2×4=4
×2×4=4
故选A.


科目:初中数学 来源: 题型:
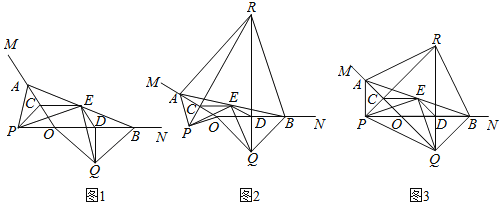
【题目】如图1,A,B分别在射线OM,ON上,且∠MON为钝角,现以线段OA,OB为斜边向∠MON的外侧作等腰直角三角形,分别是△OAP,△OBQ,点C,D,E分别是OA,OB,AB的中点.
(1)求证:△PCE≌△EDQ;
(2)延长PC,QD交于点R.
①如图2,若∠MON=150°,求证:△ABR为等边三角形;
②如图3,若△ARB∽△PEQ,求∠MON大小和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程 (a+2b)x2-2![]() x+
x+![]() (a+2b)=0有实数根.
(a+2b)=0有实数根.
(1)若a=2,b=1,求方程的根
(2)若m=a2+b2+5a,若b<0,求m的取值范围.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒.
现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒.
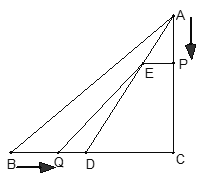
(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在BD(不包括点B、D)上移动时,设![]() 的面积为
的面积为![]() ,求
,求![]() 与月份
与月份![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 为何值时,
为何值时,![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
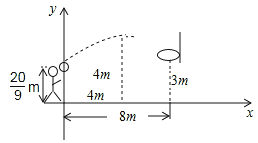
【题目】小明跳起投篮,球出手时离地面![]() m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高度4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.
m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高度4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.
(1)求此抛物线对应的函数关系式;
(2)此次投篮,球能否直接命中篮筐中心?若能,请说明理由;若不能,在出手的角度和力度都不变的情况下,球出手时距离地面多少米可使球直接命中篮筐中心?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文明小区50平方米和80平方米两种户型的住宅,50平方米住宅套数是80平方米住宅套数的2倍.物管公司月底按每平方米2元收取当月物管费,该小区全部住宅都人住且每户均按时全额缴纳物管费.
(1)该小区每月可收取物管费90 000元,问该小区共有多少套80平方米的住宅?
(2)为建设“资源节约型社会”,该小区物管公司5月初推出活动一:“垃圾分类送礼物”,50平方米和80平方米的住户分别有40%和20%参加了此次括动.为提离大家的积扱性,6月份准备把活动一升级为活动二:“拉圾分类抵扣物管费”,同时终止活动一.经调査与测算,参加活动一的住户会全部参加活动二,参加活动二的住户会大幅增加,这样,6月份参加活动的50平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() ;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加
;6月份参加活动的80平方米的总户数在5月份参加活动的同户型户数的基础上将增加![]() ,每户物管费将会减少
,每户物管费将会减少![]() .这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少
.这样,参加活动的这部分住户6月份总共缴纳的物管费比他们按原方式共缴纳的物管费将减少![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
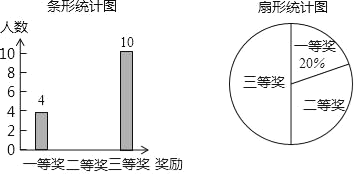
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)如果该校八年级有800人,请你估计获奖的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
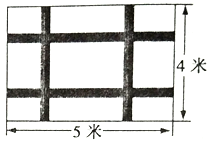
【题目】如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的![]() .
.
(1)求配色条纹的宽度;
(2)如果地毯配色条纹部分每平方米造价200元,其余部分每平方米造价100元,求地毯的总造价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com