

分析 (1)由旋转的性质得到△ADP为等边三角形,从而判断出△BPD为直角三角形,根据勾股定理计算即可;
(2)由旋转的性质得到△DAP是等边三角形,根据勾股定理的逆定理判断出△BPD为直角三角形,即可;
(3)作出△ABQ∽△ACP,判断出△APQ为直角三角形,从而得到△BPQ为直角三角形,根据勾股定理计算即可.
解答 解:(1)把△APC绕着点A顺时针旋转,使点C旋转到点B,得到△ADB,连结DP.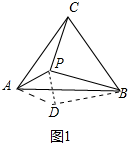
由旋转可知AD=AP,BD=PC,∠DAB=∠PAC,
∴∠DAP=∠BAC=60°,
∴△ADP为等边三角形,
∴DP=PA=3,∠ADP=60°,
∵PB=5,BD=PC=4,PD=3,
∴PD2+BD2=PB2
∴∠BDP=90°,
∴∠APC=∠ADB=∠ADP+∠PDB=60°+90°=150°.
(2)如图2,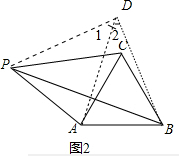
把△APC绕点A顺时针旋转,使点C与点B重合,得到△ADB,连接PD,
∴△APC≌△ADB,
∴AD=AP=3,DB=PC=4,∠PAC=∠DAB,∠APC=∠2,
∴∠DAP=∠BAC,
∵∠BAC=60°,
∴∠DAP=60°,
∴△DAP是等边三角形,
∴PD=3,∠1=60°,
∴PD2+DB2=32+42=52=PB2,
∴∠PDB=90°,
∴∠2=30°,
∴∠APC=30°;
(3)如图3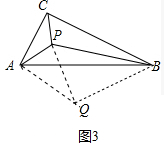
作△ABQ,使得:∠QAB=∠PAC,∠ABQ=∠ACP,则△ABQ∽△ACP,
∴∠AQB=∠APC=120°,
∵AB=2AC,
∴△ABQ与△ACP相似比为2,
∴AQ=2AP=2$\sqrt{3}$,BQ=2CP,∠QAP=∠QAB+∠BAP=∠PAC+∠BAP=∠BAC=60°,
∵$\frac{AQ}{AP}$=2,
∴∠APQ=90°,PQ=3,
∴∠AQP=30°
∴∠BQP=∠AQB-∠AQP=120°-30°=90°,
根据勾股定理得,BQ=$\sqrt{P{B}^{2}-P{Q}^{2}}$=4,
∴PC=$\frac{1}{2}$BQ=2.
点评 本题考查了旋转的性质,直角三角形的性质和判断方法,勾股定理,直角三角形的判定是解本题的关键,学会利用旋转添加辅助线,构造特殊三角形,属于中考常考题型.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
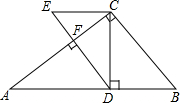 如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,DF⊥AC于F,过C作CE∥AB交DF的延长线于点E,则下列结论中错误的是( )
如图,在Rt△ACB中,∠ACB=90°,CD⊥AB于D,DF⊥AC于F,过C作CE∥AB交DF的延长线于点E,则下列结论中错误的是( )| A. | DE2=BD•AB | B. | S△CEF:S△ADF=BD2:AD2 | ||
| C. | $\frac{BD}{CA}$=$\frac{CF}{AD}$ | D. | $\frac{DF}{BC}$=$\frac{AF}{AB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知一次函数y=kx+b和y=x+a的图象交于点A,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{kx-y=-b}\\{x-y=-a}\end{array}\right.$的解为( )
已知一次函数y=kx+b和y=x+a的图象交于点A,则关于x,y的二元一次方程组$\left\{\begin{array}{l}{kx-y=-b}\\{x-y=-a}\end{array}\right.$的解为( )| A. | $\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 青岛市确定了“拥湾发展,环湾保护”的发展战略.某中学为了让学生了解环保知识,增强环保意识,举行了一次“保护胶州湾”的环保知识竞赛.共有2000名学生参加了这次竞赛,为了解本次竞赛的情况,从中抽取了部分同学的成绩作为样本进行统计.
青岛市确定了“拥湾发展,环湾保护”的发展战略.某中学为了让学生了解环保知识,增强环保意识,举行了一次“保护胶州湾”的环保知识竞赛.共有2000名学生参加了这次竞赛,为了解本次竞赛的情况,从中抽取了部分同学的成绩作为样本进行统计.| 分组 | 频数 | 频率 |
| A组:50.5~60.5 | 16 | 0.08 |
| B组:60.5~70.5 | 0.16 | |
| C组:70.5~80.5 | 40 | 0.20 |
| D组:80.5~90.5 | 64 | 0.32 |
| E组:90.5~100 | 48 | |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com