
分析 (1)根据平方和数的定义即可求解;
(2)根据双倍积数的定义即可求解;
(3)根据平方和数的定义可得a2+b2=585,根据双倍积数的定义2ab=504,再利用完全平方公式与平方差公式即可求解.
解答 解:(1)∵8=4+4=22+22,
∴该三位整数是282.
故答案为282;
(2)∵4=2×1×2=2×2×1,
∴该三位整数是142或241.
故答案为142或241;
(3)∵$\overline{a585b}$为一个平方和数,
∴a2+b2=585,
∵$\overline{a504b}$为一个双倍积数,
∴2ab=504,
∴a2+b2+2ab=585+504=1089,a2+b2-2ab=585-504=81,
∴a+b=33,a-b=9,
∴a2-b2=(a+b)(a-b)=33×9=297.
点评 本题考查了因式分解的应用,学生的阅读理解能力与知识的迁移能力,理解平方和数与双倍积数的定义是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
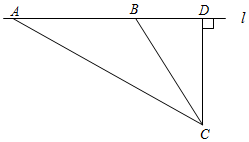 某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知P为等边△ABC内的一点,且PA=5,PB=3,PC=4,将线段BP绕点P按逆时针方向旋转60°至PQ的位置.
如图,已知P为等边△ABC内的一点,且PA=5,PB=3,PC=4,将线段BP绕点P按逆时针方向旋转60°至PQ的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com