
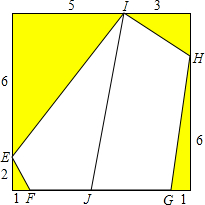
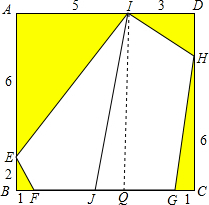
 在正方形ABCD中,切去四个三角形得到一个五边形EFGHI(如图,其中所标的数表示各线段的长度),线段IJ将五边形EFGHI分成两个面积相等的部分,那么FJ的长度是
在正方形ABCD中,切去四个三角形得到一个五边形EFGHI(如图,其中所标的数表示各线段的长度),线段IJ将五边形EFGHI分成两个面积相等的部分,那么FJ的长度是| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 13 |
| 4 |
| 13 |
| 4 |


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
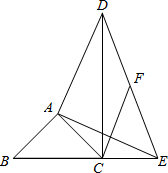 已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE.
已知:如图,在△ABC中,∠BAC=90°,AB=AC,点E在边BC的延长线上,DA⊥AE,AD=AE.查看答案和解析>>
科目:初中数学 来源: 题型:
 2011年3月2日,宁波召开打通“断头路”专项行动部署,并指出:力争通过3年努力打造59条城区“断头路”,在某一条“断头路”工程中,修筑的公路长度y(米)与时间x(天)之间的关系图象.根据图象提供的信息,可知该公路的长度是
2011年3月2日,宁波召开打通“断头路”专项行动部署,并指出:力争通过3年努力打造59条城区“断头路”,在某一条“断头路”工程中,修筑的公路长度y(米)与时间x(天)之间的关系图象.根据图象提供的信息,可知该公路的长度是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com