练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

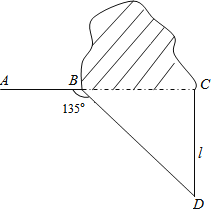
    【题目】如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（≈1.414，精确到1米）

    【答案】直线L上距离D点566米的C处开挖．

    【解析】

    试题由已知条件易得△BCD是等腰直角三角形，再根据勾股定理可得CD2+BC2=BD2，由BD=800米代入进行计算即可

    试题解析：∵CD⊥AC，

    ∴∠ACD=90°，

    ∵∠ABD=135°，

    ∴∠DBC=45°，

    ∴∠D=45°，

    ∴CB=CD，

    在Rt△DCB中：CD2+BC2=BD2，

    2CD2=8002，

    CD=400≈566（米），

    答：直线L上距离D点566米的C处开挖．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下面的解题过程：

    计算：（－15）÷（－1－3）×6.

    解：原式＝（－15）÷（－）×6（第一步）

    ＝（－15）÷（－25）（第二步）

    ＝.（第三步）

    解答：（1）上面解题过程，从第____步开始错误，错误的原因是_____.

    （2）请写出正确的解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算下面各题
    （1）计算：
    （2）先化简．再求值：a（a﹣2b）+2（a+b）（a﹣b）+（a+b）2 ， 其中a=﹣ ，b=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】衢州市新农村建设推动了农村住宅旧貌变新颜，如图为一农村民居侧面截图，屋坡AF、AG分别架在墙体的点B、点C处，且AB=AC，侧面四边形BDEC为矩形．若测得∠FAG=110°，则∠FBD=（ ）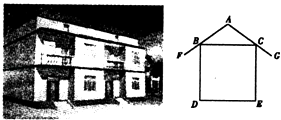
    A.35°
    B.40°
    C.55°
    D.70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝CB，∠ABC＝90°，D为AB延长线上一点，点E在BC边上，且BE＝BD，连结AE、DE、DC．

    ① 求证：△ABE≌△CBD；

    ② 若∠CAE＝30°，求∠BDC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】月球是地球的近邻，它的起源一直是人类不断探索的谜题之一．全球迄今进行了126次月球探测活动，因为研究月球可提高人类对宇宙的认识，包括认识太阳系的演化及特点，认识地球自然系统与太空自然现象之间的关系．我们已经认识到，在月球表面，白天阳光垂直照射的地方温度高达127℃，夜晚温度可降到﹣183℃．下面对“﹣183℃”的叙述不正确的是（　　）

    A. ﹣183是一个负数

    B. ﹣183表示在海平面以下183米

    C. ﹣183在数轴上的位置在原点的左边

    D. ﹣183是一个比﹣100小的数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，下列条件：①∠1=∠2，②∠3+∠4=180°，③∠5+∠6=180°，④∠2=∠3，⑤∠7=∠2+∠3，⑥∠7+∠4-∠1=180°中能判断直线∥的有（ ）

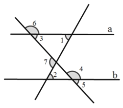
    A. 3个 B. 4个 C. 5个 D. 6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有足够多的长方形和正方形卡片，如下图：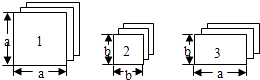
    （1）如果选取1号、2号、3号卡片分别为1张、2张、3张，可拼成一个长方形（不重叠无缝隙），请画出这个长方形的草图，并运用拼图前后面积之间的关系说明这个长方形的代数意义．
    这个长方形的代数意义是 ．
    （2）小明想用类似方法解释多项式乘法（a+3b）（2a+b）=2a2+7ab+3b2 ， 那么需用2号卡片张，3号卡片张．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的情景对话，然后解答问题：

    （1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？
    （2）在Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b＞a，若Rt△ABC是奇异三角形，求a：b：c；
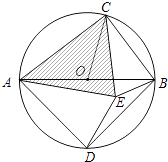
    （3）如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆 的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE． ①求证：△ACE是奇异三角形；
    ②当△ACE是直角三角形时，求∠AOC的度数．

    查看答案和解析>>

    同步练习册答案