
【题目】如图所示,AB是⊙O的直径,点C是弧AB的中点,点D是弧BC的中点,连接AC,BC,AD,BD,且AD与BC相交于点F,延长AC至E,使AC=EC,连接EB交AD的延长线于点G.
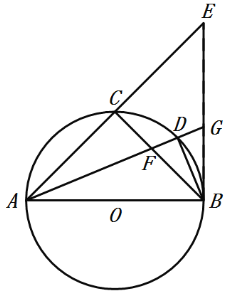
(1)求证:EB是⊙O的切线;
(2)求证;AF=2BD;
(3)求证:线段BG是线段CF和线段EG的比例中项.
【答案】(1)详见解析;(2)详见解析;(3)详见解析
【解析】
(1)由“SAS”可证△ABC≌△EBC,可得∠ABC=∠EBC=45°,可得∠EBA=90°,即可得结论;
(2)延长BD交AE于点M,由“ASA”可证△ADB≌△ADM和△ACF≌△BCM,可得BD=DM,AF=BM=2BD;
(3)过点F作FN⊥AB,过点G作GK⊥AE,由等腰三角形的性质和直角三角形的性质可得BF=![]() CF,EG=
CF,EG=![]() KG=
KG=![]() BG=
BG=![]() BF,即可得结论.
BF,即可得结论.
证明:(1)∵AB是⊙O 的直径,
∴∠ACB=90°
又∵点C是弧AB的中点,
∴∠ABC=45°
又∵AC=EC,∠ACB=∠ECB=90°,BC=BC
∴△ABC≌△EBC(SAS)
∴∠ABC=∠EBC=45°
∴∠EBA=90°,且AB是⊙O 的直径
∴EB是⊙O的切线.
(2)如图,延长BD交AE于点M
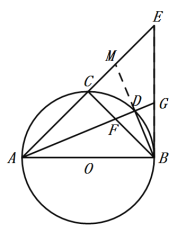
∵AB是⊙O 的直径
∴∠ACB=90°,∠ADB=90°
∵点D是弧BC的中点
∴∠MAD=∠BAD=![]() ∠BAC=22.5°,且∠ADB=∠ADM=90°,AD=AD
∠BAC=22.5°,且∠ADB=∠ADM=90°,AD=AD
∴△ADB≌△ADM(ASA)
∴BD=DM
∴BM=2BD
∵点C是弧AB的中点
∴AC=BC,∠ACF=∠BCM=90°,∠CBD=∠CAD
∴△ACF≌△BCM(AAS)
∴AF=BM
∴AF=2BD.
(3)如图,过点F作FN⊥AB,过点G作GK⊥AE,垂足分别为N,K,
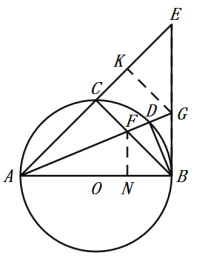
由(2)可知∠CAD=∠BAD=22.5°,∠ABC=∠E=45°,
∴∠BFD=∠BAF+∠ABF=22.5°+45°=67.5°,∠BGF=∠CAD+∠E=22.5°+45°=67.5°,
∴∠BFD=∠BGF,
∴BF=BG,
∵∠CAF=∠NAF,FC⊥AE,FN⊥AB,
∴NF=CF,
又∵∠ABC=45°,∠FNB=90°,
∴NF=BN=CF,
∴![]() ,
,
同理![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴BF是线段CF和线段EG的比例中项.
即线段BG是线段CF和线段EG的比例中项.


科目:初中数学 来源: 题型:
【题目】已知OABC的顶点O与坐标原点重合,点A在x轴正半轴上,点B的坐标为(3,4),且B,C不在同一象限内,若反比例函数y=![]() 的图象经过线段AB的中点D,则四边形ODBC的面积为____.
的图象经过线段AB的中点D,则四边形ODBC的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC为矩形,OA=4,OC=5,正比例函数y=2x的图像交AB于点D,连接DC,动点Q从D点出发沿DC向终点C运动,动点P从C点出发沿CO向终点O运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了t s.
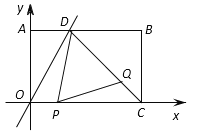
(1)求点D的坐标;
(2)若PQ∥OD,求此时t的值?
(3)是否存在时刻某个t,使S△DOP=![]() S△PCQ?若存在,请求出t的值,若不存在,请说明理由;
S△PCQ?若存在,请求出t的值,若不存在,请说明理由;
(4)当t为何值时,△DPQ是以DQ为腰的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初期,天气炎热,水杯需求量大.双福育才中学门口某超市购进一批水杯,其中A种水杯进价为每个15元,售价为每个25元;B种水杯进价为每个12元,售价为每个20元
(1)该超市平均每天可售出60个A种水杯,后来经过市场调查发现,A种水杯单价每降低1元,则平均每天的销量可增加10个.为了尽量让学生得到更多的优惠,某天该超市将A种水杯售价调整为每个m元,结果当天销售A种水杯获利630元,求m的值.
(2)该超市准备花费不超过1600元的资金,购进A、B两种水杯共120个,其中B种水杯的数量不多于A种水杯数量的两倍.请为该超市设计获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点E是正方形ABCD中边AB的中点.
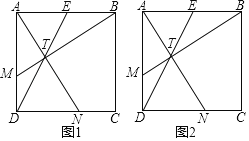
(1)如图1,点T为线段DE上一点,连接BT并延长交AD于点M,连接AT并延长交CD于点N,且AM=DN.试判断线段AN与线段BM的关系,并证明;求证:点M是线段AD的黄金分割点.
(2)如图2,在AD边上取一点M,满足AM2=DMDA时,连接BM交DE于点T,连接AT并延长交DC于点N,求tan∠MTD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
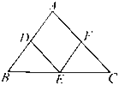
【题目】如图,在![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,则下列四个判断中不一定正确的是()
的中点,则下列四个判断中不一定正确的是()
A. 四边形![]() 一定是平行四边形
一定是平行四边形
B. 若![]() ,则四边形
,则四边形![]() 是矩形
是矩形
C. 若四边形![]() 是菱形,则
是菱形,则![]() 是等边三角形
是等边三角形
D. 若四边形![]() 是正方形,则
是正方形,则![]() 是等腰直角三角形
是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与 △ADE中,∠ACB=∠AED=90°,连接BD、CE,∠EAC=∠DAB.
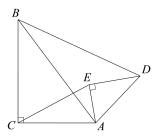
(1)求证:△ABC ∽△ADE;
(2)求证:△BAD ∽△CAE;
(3)已知BC=4,AC=3,AE=![]() .将△AED绕点A旋转,当点E落在线段CD上时,求 BD的长.
.将△AED绕点A旋转,当点E落在线段CD上时,求 BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com