
【题目】在下述命题中,真命题有( )
(1)对角线互相垂直的四边形是菱形
(2)三个角的度数之比为1:3:4的三角形是直角三角形
(3)对角互补的平行四边形是矩形
(4)三边之比为1: ![]() :2的三角形是直角三角形.
:2的三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:(1)对角线平分且互相垂直的四边形是菱形,故错误;(2)180°÷8×4=90°,故正确;(3)∵平行四边形的对角相等,又互补,
∴每一个角为90°
∴这个平行四边形是矩形,故正确;(4)设三边分别为x, ![]() x:2x,
x:2x,
∵x2+( ![]() x)2=(2x)2 ,
x)2=(2x)2 ,
∴由勾股定理的逆定理得,
这个三角形是直角三角形,故正确;
真命题有3个,故选C.
【考点精析】关于本题考查的勾股定理的逆定理和菱形的判定方法,需要了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
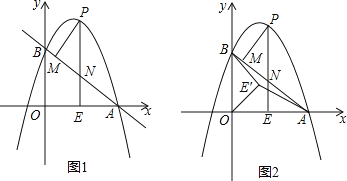
【题目】如图1,抛物线![]() 与
与![]() 轴交于点A(4,0),与
轴交于点A(4,0),与![]() 轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作
轴交于点B,在x轴上有一动点E(m,0)(0<m<4),过点E作![]() 轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
轴的垂线交直线AB于点N,交抛物线于点P,过点P作PM⊥AB于点M.
(1)求![]() 的值和直线AB的函数表达式;
的值和直线AB的函数表达式;
(2)在P点运动的过程中,请用含m的代数式表示线段PN;
(3)设△PMN的周长为![]() ,△AEN的周长为
,△AEN的周长为![]() ,若
,若![]() ,求m的值;
,求m的值;
(4)如图2,在(3)条件下,将线段OE绕点O逆时针旋转得到OE′,旋转角为α(0°<α<90°),连接![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件夹克衫先按成本提高50%标价,再以8折(标价的80%)出售,结果获利20元,若设这件夹克衫的成本是x元,根据题意,可得到的方程是( )
A.(1+50%)x×80%=x﹣20
B.(1+50%)x×80%=x+20
C.(1+50%x)×80%=x﹣20
D.(1+50%x)×80%=x+20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式不能使用平方差公式的是( )
A. (2a+b)(2a﹣b) B. (﹣2a+b)(b﹣2a)
C. (﹣2a+b)(﹣2a﹣b) D. (2a﹣b)﹣(2a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一两位数,其十位数字为a,个位数字为b,将两个数颠倒,得到一个新的两位数,那么这个新两位数十位上的数字与个位数字的和与这个新两位数的积用代数式表示( )
A.ba(a+b)
B.(a+b)(b+a)
C.(a+b)(10a+b)
D.(a+b)(10b+a)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com