

·ÖĪö £Ø1£©”÷ABCŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬ĄūÓĆSAS¼“æÉÖ¤Ć÷”÷BAD”Õ”÷CAF£¬“Ó¶ųÖ¤µĆCF=BD£¬¾Ż“Ė¼“æÉÖ¤µĆ£»
£Ø2£©Ķ¬£Ø1£©ĻąĶ¬£¬ĄūÓĆSAS¼“æÉÖ¤µĆ”÷BAD”Õ”÷CAF£¬“Ó¶ųÖ¤µĆBD=CF£¬¼“æɵƵ½CF-CD=BC£»
£Ø3£©Ź×ĻČÖ¤Ć÷”÷BAD”Õ”÷CAF£¬”÷FCDŹĒÖ±½ĒČż½ĒŠĪ£¬Č»ŗóøł¾ŻÕż·½ŠĪµÄŠŌÖŹ¼“æÉĒóµĆDFµÄ³¤£¬ŌņOC¼“æÉĒóµĆ£®
½ā“š ½ā£ŗ£Ø1£©”ß”ĻBAC=90”ć£¬”ĻABC=45”ć£¬
”ą”ĻACB=”ĻABC=45”ć£¬
”ąAB=AC£¬
”ßĖıߊĪADEFŹĒÕż·½ŠĪ£¬
”ąAD=AF£¬”ĻDAF=90”ć£¬
”ß”ĻBAD=90”ć-”ĻDAC£¬”ĻCAF=90”ć-”ĻDAC£¬
”ą”ĻBAD=”ĻCAF£¬
ŌņŌŚ”÷BADŗĶ”÷CAFÖŠ£¬
$\left\{\begin{array}{l}{AB=AC}\\{”ĻBAD=”ĻCAF}\\{AD=AF}\end{array}\right.$£¬
”ą”÷BAD”Õ”÷CAF£ØSAS£©£¬
”ąBD=CF£¬
”ßBD+CD=BC£¬
”ąCF+CD=BC£»
¹Ź“š°øĪŖ£ŗCF+CD=BC£»
£Ø2£©”ßĖıߊĪADEFĪŖÕż·½ŠĪ£¬
”ąAD=AF£¬”ĻDAF=90”ć
”ß”ĻBAC=90”ć£¬
”ą”ĻBAC+”ĻDAC=”ĻDAF+”ĻDAC£¬
¼“”ĻBAD=”ĻCAF£¬
ŌŚ”÷ABDŗĶ”÷ACFÖŠ£¬$\left\{\begin{array}{l}{AB=AC}\\{”ĻBAD=”ĻCAF}\\{AD=AF}\end{array}\right.$£¬
”ą”÷ABD”Õ”÷ACF£ØSAS£©£¬
”ąBD=CF£¬
”ąCF=BC+CD£»
£Ø3£©”ß”ĻBAC=90”ć£¬”ĻABC=45”ć£¬
”ą”ĻACB=”ĻABC=45”ć£¬
”ąAB=AC£¬
”ßĖıߊĪADEFŹĒÕż·½ŠĪ£¬
”ąAD=AF£¬”ĻDAF=90”ć£¬
”ß”ĻBAD=90”ć-”ĻBAF£¬”ĻCAF=90”ć-”ĻBAF£¬
”ą”ĻBAD=”ĻCAF£¬
”ßŌŚ”÷BADŗĶ”÷CAFÖŠ£¬
$\left\{\begin{array}{l}{AB=AC}\\{”ĻBAD=”ĻCAF}\\{AD=AF}\end{array}\right.$£¬
”ą”÷BAD”Õ”÷CAF£ØSAS£©£¬
”ą”ĻACF=”ĻABD£¬
”ß”ĻABC=45”ć£¬
”ą”ĻABD=135”ć£¬
”ą”ĻACF=”ĻABD=135”ć£¬
”ą”ĻFCD=90”ć£¬
”ą”÷FCDŹĒÖ±½ĒČż½ĒŠĪ£®
”ßÕż·½ŠĪADEFµÄ±ß³¤ĪŖ2$\sqrt{2}$ĒŅ¶Ō½ĒĻßAE”¢DFĻą½»ÓŚµćO£®
”ąDF=$\sqrt{2}$AD=4£¬OĪŖDFÖŠµć£®
”ąOC=$\frac{1}{2}$DF=2£®
µćĘĄ ±¾Ģāæ¼²éĮĖÕż·½ŠĪµÄŠŌÖŹ£¬Č«µČČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬µČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹ£¬µČŃüČż½ĒŠĪµÄÅŠ¶Ø£¬ŅŌ¼°Ķ¬½ĒµÄÓą½ĒĻąµČµÄŠŌÖŹ£¬“ĖĄąĢāÄæĶس£¶¼ŹĒÓĆĶ¬Ņ»ÖÖĖ¼Ā·Ēó½ā£¬ŌŚ£Ø1£©ÖŠÕŅ³öÖ¤Ć÷Čż½ĒŠĪČ«µČµÄĖ¼Ā·ŹĒ½āĢāµÄ¹Ų¼ü£®


 ŠÄĖćæŚĖćĒÉĖćŅ»æĪŅ»Į·ĻµĮŠ“š°ø
ŠÄĖćæŚĖćĒÉĖćŅ»æĪŅ»Į·ĻµĮŠ“š°ø Ó¦ÓĆĢā×÷Ņµ±¾ĻµĮŠ“š°ø
Ó¦ÓĆĢā×÷Ņµ±¾ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
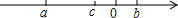 ŅŃÖŖÓŠĄķŹża£¬b£¬cŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£ŗ»Æ¼ņ$\frac{|abc|}{abc}+\frac{a+b+c}{|a+b+c|}-\frac{|bc|}{bc}-\frac{c-b}{|c-b|}-\frac{a}{|a|}$£®
ŅŃÖŖÓŠĄķŹża£¬b£¬cŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£ŗ»Æ¼ņ$\frac{|abc|}{abc}+\frac{a+b+c}{|a+b+c|}-\frac{|bc|}{bc}-\frac{c-b}{|c-b|}-\frac{a}{|a|}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
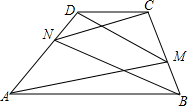 ČēĶ¼£¬ĢŻŠĪABCDÖŠAB”ĪCD£¬AB£¾CD£¬N”¢M·Ö±šŹĒŃüAD”¢CBÉĻµÄµć£¬ŅŃÖŖ”ĻDAM=”ĻCBN£®ĒóÖ¤£ŗ”ĻDMA=”ĻCNB£®
ČēĶ¼£¬ĢŻŠĪABCDÖŠAB”ĪCD£¬AB£¾CD£¬N”¢M·Ö±šŹĒŃüAD”¢CBÉĻµÄµć£¬ŅŃÖŖ”ĻDAM=”ĻCBN£®ĒóÖ¤£ŗ”ĻDMA=”ĻCNB£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com