
 如图所示,炮兵在地面C点观察到空中B点有一架敌机,仰角为45°,敌机在同一高度作直线飞行,经过D点到达A点时炮兵观测的仰角为30°,而D点位于炮兵阵地C的正上方2000米处,该敌机从B点飞到A点用1分钟,求敌机的飞行速度.
如图所示,炮兵在地面C点观察到空中B点有一架敌机,仰角为45°,敌机在同一高度作直线飞行,经过D点到达A点时炮兵观测的仰角为30°,而D点位于炮兵阵地C的正上方2000米处,该敌机从B点飞到A点用1分钟,求敌机的飞行速度. 分析 作CD⊥AB于点D,则CD=2000米,利用三角函数定义分别求出BD和AD的长,根据AB=BD+AD求得AB的长,再根据速度=路程÷时间即可求解.
解答 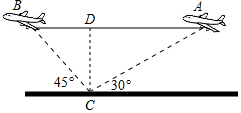 解:作CD⊥AB于点D,则CD=2000米.
解:作CD⊥AB于点D,则CD=2000米.
∵在Rt△BCD中,∠B=45°,
∴BD=CD=2000米,
∵在Rt△ACD中,∠A=30°,
∴AD=$\sqrt{3}$CD=2000$\sqrt{3}$米.
∴AB=BD+AD=2000+2000$\sqrt{3}$,
∵该敌机从B点飞到A点用1分钟,即60秒,
∴敌机的飞行速度为(2000+2000$\sqrt{3}$)÷60=$\frac{100+100\sqrt{3}}{3}$(米/秒).
答:敌机的飞行速度为$\frac{100+100\sqrt{3}}{3}$米/秒.
点评 本题考查了解直角三角形的应用,锐角三角函数,理解题意准确画出图形,求出BD和AD的长是解题的关键.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:填空题
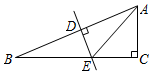 如图,Rt△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE=3$\sqrt{2}$.
如图,Rt△ABC中,∠C=90°,∠B=22.5°,AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE=3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是40°.
如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠FPE=100°,则∠PFE的度数是40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
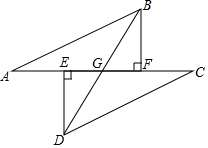 已知:如图点A,E,F,C在同一直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,连接AB,CD,BD,BD交AC于点G,若AB=CD,求证:△DEG≌△BFG.
已知:如图点A,E,F,C在同一直线上,AE=CF,过E,F分别作DE⊥AC,BF⊥AC,连接AB,CD,BD,BD交AC于点G,若AB=CD,求证:△DEG≌△BFG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com