Question

5．如图，抛物线y=-x²+（1-m）x-m²+12交x轴于点A，交y轴于点B（0，3），顶点C位于第二象限，连结AB，AC，BC．
（1）求抛物线的解析式；
（2）在x轴上是否存在点P，使得△PAB的面积等于△ABC的面积？如果存在，求出P点坐标；
（3）将△ABC沿x轴向右平移t个单位长度（0＜t＜1）时，平移后△ABC与△ABO重叠部分的面积为S，求S与t之间的函数关系式．

Answer 1

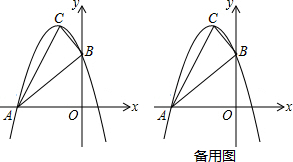
分析 （1）把B坐标代入抛物线解析式求出m的值，确定出抛物线解析式即可；
（2）由抛物线解析式确定出A，B，C的坐标，进而求出AC，BC，AB的长，利用勾股定理的逆定理确定出三角形ABC为直角三角形，由三角形PAB与三角形ABC面积相等求出AP的长，确定出P坐标即可；
（3）如图所示，画出平移后的三角形为△A′B′C′，A′C′与AB交于M点，A′B′与y轴交于N点，根据A′坐标及A′C′∥AC，得到两直线斜率相等，表示出直线A′C′解析式，与直线AB联立求出M坐标，进而表示出三角形AA′M面积，再求出三角形A′ON面积，由三角形AOB面积减去三角形AA′M，再减去三角形A′ON面积，求出重叠部分面积即可．

解答 解：（1）把B（0，3）代入解析式得：-m²+12=3，
解得：m=3或m=-3，
∵1-m＜0，
∴m=3，
则抛物线解析式为y=-x²-2x+3；
（2）由抛物线解析式可得A（-3，0），C（-1，4），B（0，3），
∴AC=2$\sqrt{5}$，BC=$\sqrt{2}$，AB=3$\sqrt{2}$，
∴AC²=BC²+AB²，
∴∠ABC=90°，
∴S_△PAB=S_△ABC=$\frac{1}{2}$×AB×BC=$\frac{1}{2}$×AP×OB，
解得：AP=$\sqrt{2}$×3$\sqrt{2}$÷3=2，
则P（-1，0）或P（-5，0）；
（3）如图所示，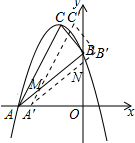

记平移后的三角形为△A′B′C′，A′C′与AB交于M点，A′B′与y轴交于N点，
∵A′（-3+t，0），A′C′∥AC，k_AC=2，
∴直线A′C′解析式为y=2x+6-2t，
∵直线AB解析式为y=x+3，
∴M（-3+2t，2t），
∴S_△AA′M=$\frac{1}{2}$×AA′×y_M=$\frac{1}{2}$t×2t=t²，
∵A′B′∥AB，
∴S_△OA′N=$\frac{1}{2}$OA′²=$\frac{1}{2}$（3-t）²，
∴S_重叠=S_△ABO-S_△A′NO-S_△AA′M=-$\frac{3}{2}$t²+3t．

点评 此题属于二次函数综合题，涉及的知识有：待定系数法确定抛物线解析式，勾股定理的逆定理，平移的性质，平行线的性质，两直线的交点，以及三角形面积求法，熟练掌握性质及定理是解本题的关键．