
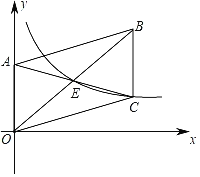
【题目】如图,已知平面直角坐标系中A点坐标为(0,4),以OA为一边在第一象限作平行四边形OABC,对角线AC、OB相交于点E,AB=2OA.若反比例函数y=![]() 的图象恰好经过点C和点E,则k的值为______.
的图象恰好经过点C和点E,则k的值为______.
【答案】![]()
【解析】
过点C作CD⊥x轴于点D,由已知条件及平行四边形的性质可得BC=OA=4,OC=AB=8,设C(x,![]() ),则点E(
),则点E(![]() ,
,![]() ),点B(x,
),点B(x,![]() +4),分别按照点E在反比例函数图象上和作为线段BD的中点,用两种方式表示出点E的纵坐标,从而得到关于x和k的等式,解得x和k的关系,再在Rt△COD中,由勾股定理得关于k的方程,解得k的值,舍去负值,即可得出答案.
+4),分别按照点E在反比例函数图象上和作为线段BD的中点,用两种方式表示出点E的纵坐标,从而得到关于x和k的等式,解得x和k的关系,再在Rt△COD中,由勾股定理得关于k的方程,解得k的值,舍去负值,即可得出答案.
解:如图,过点C作CD⊥x轴于点D,
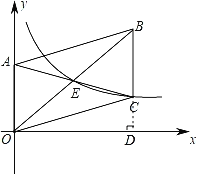
∵A点坐标为(0,4),AB=2OA.
∴OA=4,AB=8,
∵四边形OABC为平行四边形,
∴BC=OA=4,OC=AB=8,点B、C、D共线,
∵反比例函数y=![]() 的图象恰好经过点C和点E,
的图象恰好经过点C和点E,
∴设C(x,![]() ),则点E(
),则点E(![]() ,
,![]() ),点B(x,
),点B(x,![]() +4),
+4),
∵E为平行四边形对角线的交点,
∴E为OB中点,
∴点E的坐标又可以表示为:(![]() ,
,![]() +2),
+2),
∴![]() =
=![]() +2,
+2,
解得:![]() =
=![]() ,
,
∴x=![]() ,
,
∴在Rt△COD中,由勾股定理得:
![]() +
+![]() =64,
=64,
解得k=![]() .(负值舍去,因为反比例函数图象位于第一象限).
.(负值舍去,因为反比例函数图象位于第一象限).
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是斜边AB上的中线,以
是斜边AB上的中线,以![]() 为直径的
为直径的![]() 分别交于
分别交于![]() 点
点![]() ,过点N作
,过点N作![]() ,垂足为
,垂足为![]() .
.
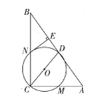
(1)求证:![]() 与
与![]() 相切;
相切;
(2)若![]() 半径为
半径为![]() ,
,![]() ,则
,则![]() 的长为_______________;
的长为_______________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中仼意三个相邻格子中所填整数之和都相等.
|
|
|
| 5 | 4 | …… |
(1)可求得![]() _____;
_____;![]() _____;
_____;![]() _____.
_____.
(2)第2019个格子中的数为______;
(3)前2020个格子中所填整数之和为______.
(4)前![]() 个格子中所填整数之和是否可能为2020?若能,求出
个格子中所填整数之和是否可能为2020?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AB=6,AC=8,D 为 AC 上一点,将△ABD 沿 BD 折叠,使点 A 恰好落在 BC 上的 E 处,则折痕 BD 的长是( )

A.5B.![]() C.3
C.3 ![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁5辆客车前往宁波东站接员工返岗.已知现有A、B两种客车,A型客车的载客量为45人/辆,每辆租金为400元;B型客车的载客量为30人/辆,每辆租金为280元.设租用A型客车为x辆,所需费用为y元.
(1)求y关于x的函数解析式;
(2)若该企业需要接的员工有205人,请求出租车费用最小值,并写出对应的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
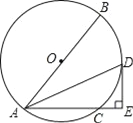
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
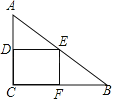
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的顶点E在边AB上,D,F两点分别在边AC,BC上,且![]() ,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
A.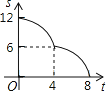 B.
B.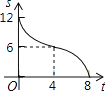 C.
C. D.
D.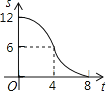
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,曲线
中,曲线![]() 经过点
经过点![]() ,直线
,直线![]() 与曲线
与曲线![]() 围成的封闭区域为图象
围成的封闭区域为图象![]() .
.
(1)求曲线![]() 的表达式;
的表达式;
(2)求出直线与曲线的交点坐标;
(3)直接写出图象![]() 上的整数点个数有_________个,它们是___________.
上的整数点个数有_________个,它们是___________.
(注:横,纵坐标均为整数的点称为整点,图象![]() 包含边界)
包含边界)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
,与x轴交于两点A,B(点A在点B的左侧),与y轴交于点C.
(Ⅰ)求点A,B和点C的坐标;
(Ⅱ)已知P是线段![]() 上的一个动点.
上的一个动点.
①若![]() 轴,交抛物线于点Q,当
轴,交抛物线于点Q,当![]() 取最大值时,求点P的坐标;
取最大值时,求点P的坐标;
②求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com