解:(1)如图,∵两条直线相交,最多有1个交点,
三条直线相交,最多有1+2=3个交点,
四条直线相交,最多有1+2+3=6个交点.
∴五条直线相交,最多有1+2+3+4=10个交点;
(2)n条直线相交,最多有1+2+3+…+(n-1)=

个交点;
(3)10条直线相交,最多有
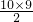
=45个交点;
(4)会出现31个交点,如下图所示:

分析:(1)要探求相交直线的交点的最多个数,则应尽量让每两条直线产生不同的交点.根据两条直线相交有一个交点,画第五条直线时,应尽量和前面四条直线都产生交点,即增加4个交点,则有6+4=10个交点;
(2)根据已知条件,求得n条直线相交,最多有1+2+3+…+(n-1)=

个交点;
(3)将n=10代入上式即可求解;
(4)可使5条直线平行,另3条直线平行且都与这5条相交,再有2条直线平行且都与这5条直线相交,且3条和2条也有相交.
点评:此题考查平面内不重合直线的位置关系,是寻找规律的题型,找到n条直线相交,最多有

个交点是解题的关键.


 个交点;
个交点;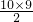 =45个交点;
=45个交点;
 个交点;
个交点; 个交点是解题的关键.
个交点是解题的关键. 

