
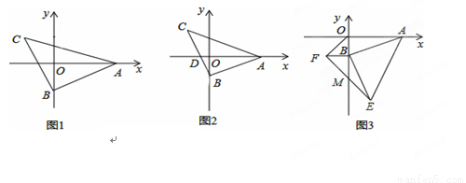
(本题8分)已知△ABC中,∠ABC=90゜,AB=BC,点A、B分别是x轴和y轴上的一动点.
(1)如图1,若点C的横坐标为-4,求点B的坐标;
(2)如图2,BC交x轴于D,若点C的纵坐标为3,A(5,0),求点D的坐标.
(3)如图3,分别以OB、AB为直角边在第三、四象限作等腰直角△OBF和等腰直角△ABE,EF交y轴于M,求 S△BEM:S△ABO.
【解析】
(1)如图1,作CM⊥y轴于M,则CM=4,
∵∠ABC=∠AOB=90゜,
∴∠CBM+∠ABO=90°,∠ABO+∠OAB=90°,
∴∠CBM=∠BAO,
在△BCM和△ABO中

∴△BCM≌△ABO(AAS),
∴OB=CM=4,
∴B(0,-4).
(2)如图2,作CM⊥y轴,
∵∠CBO+∠OBA=∠CBA=90°,
∠OBA+∠BAO=90°,
在△CMB和△BOA中,

∴△CMB≌△BOA(AAS),
∴CM=BO,AO=BM,
∵点C的纵坐标为3,
∴MO=3,
∴CM=BO=BM-MO=5-3=2,
∵CM⊥y轴,
∴△BDO∽△BCM,
∴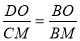 ,
,
即DO=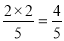
故点D的坐标为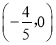
(3)如图3,作EN⊥y轴于N,
∵∠ENB=∠BOA=∠ABE=90°,
∴∠OBA+∠NBE=90°,∠OBA+∠OAB=90°,
∴∠NBE=∠BAO,
在△ABO和△BEN中

∴△ABO≌△BEN(AAS),
∴△ABO的面积=△BEN的面积,OB=NE=BF,
∵∠OBF=∠FBM=∠BNE=90°,
∴在△BFM和△NEM中
 ,
,
∴△BFM≌△NEM(AAS),
∴BM=NM,
∵△BME边BM上的高和△NME的边MN上的高相等,
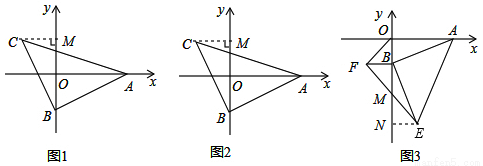
∴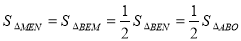 ,
,
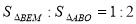 .
.
【解析】
试题分析:(1)作CM⊥y轴于M,则CM=4,求出∠ABC=∠AOB=90゜,∠CBM=∠BAO,证△BCM≌△ABO,求出OB=CM=4即可.
(2)作CM⊥y轴于M,利用AAS得到△CMB≌△BOA,得到各边长,然后由△BDO∽△BCM得到DO的长度,继而得到点D坐标;
(3)作EN⊥y轴于N,求出∠NBE=∠BAO,证△ABO≌△BEN,推出△ABO的面积=△BEN的面积,OB=NE=BF,
∵∠OBF=∠FBM=∠BNE=90°,证△BFM≌△NEM,推出BM=NM,根据三角形面积公式得出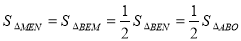 ,即可得出答案.
,即可得出答案.
考点:全等三角形的判定与性质;坐标与图形性质;等腰直角三角形.


科目:初中数学 来源:2014-2015学年江苏兴化顾庄等三校七年级上学期12月月考数学试卷(解析版) 题型:填空题
已知代数式x2+x+3的值是5,那么10-3x2-3x的值是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏兴化顾庄等三校七年级上学期12月月考数学试卷(解析版) 题型:选择题
将12000000用科学计数法表示是( )
A.12×106 B.1.2×107 C.0.12×108 D.120×105
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市八年级上学期期末数学试卷(解析版) 题型:选择题
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
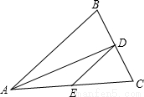
A.20 B.12 C.14 D.13
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级1月月考数学试卷(解析版) 题型:解答题
(8分)在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒. 七
年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.
(1)七年级(2)班有男生、女生各多少人?
(2)要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省深州市九年级上学期第三次月考数学试卷(解析版) 题型:选择题
如图,已知⊙O的两条弦AC、BD相交于点E,∠A=70°,∠C=50°,那么sin∠AEB的值为( )

A.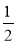 B.
B. C.
C.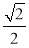 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com