
分析 根据一元二次方程必须满足四个条件,未知数的最高次数是2;二次项系数不为0;是整式方程;含有一个未知数.
解答 解:张敏的这种想法不全面,
由x2a+b-2xa-b+3=0是关于x的一元二次方程,得
$\left\{\begin{array}{l}{2a+b=2}\\{a-b=0}\end{array}\right.$或$\left\{\begin{array}{l}{2a+b=2}\\{a-b=1}\end{array}\right.$或$\left\{\begin{array}{l}{2a+b=2}\\{a-b=2}\end{array}\right.$或$\left\{\begin{array}{l}{2a+b=1}\\{a-b=2}\end{array}\right.$或$\left\{\begin{array}{l}{2a+b=0}\\{a-b=2}\end{array}\right.$.
点评 本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
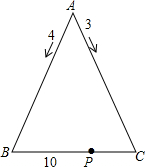 如图,有两只蚂蚁同时从一个等腰三角形的顶点A出发,先分别沿两腰爬行,速度分别为4厘米/秒,3厘米/秒,7秒后在离点B处10厘米的点P相遇,求PC的长.
如图,有两只蚂蚁同时从一个等腰三角形的顶点A出发,先分别沿两腰爬行,速度分别为4厘米/秒,3厘米/秒,7秒后在离点B处10厘米的点P相遇,求PC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com